Exploring like a Data Adventurer

Purpose of this chapter

Exploring the normality of numerical columns in a novel data set and producing publication quality tables and reports

Take-aways

  1. Using summary statistics to better understand individual columns in a data set.
  2. Assessing data normality in numerical columns.
  3. Producing a publishable HTML with summary statistics and normality tests for columns within a data set.

Required Setup

We first need to prepare our environment with the necessary packages

# Sets the number of significant figures to two - e.g., 0.01
options(digits = 2)

# Required package for quick package downloading and loading 
if (!require(pacman))
  install.packages("pacman")

pacman::p_load(dlookr, # Exploratory data analysis
               formattable, # HTML tables from R outputs
               here, # Standardizes paths to data
               kableExtra, # Alternative to formattable
               knitr, # Needed to write HTML reports
               tidyverse) # Powerful data wrangling package suite

Load and Examine a Data Set

We will be using open source data from UArizona researchers that investigates the effects of climate change on canopy trees. (Meredith, Ladd, and Werner 2021)

# Let's load a data set from the canopy tree data set
dataset <- read.csv(here("EDA_In_R_Book", "data", "Data_Fig2_Repo.csv")) 

# What does the data look like?
dataset |>
  head() |>
  formattable()
Date Group Sap_Flow TWaterFlux pLWP mLWP
10/4/19 Drought-sens-canopy 184.0 82.2 -0.26 -0.68
10/4/19 Drought-sens-under 2.5 1.3 -0.30 -0.76
10/4/19 Drought-tol-canopy 10.6 4.4 -0.44 -0.72
10/4/19 Drought-tol-under 4.4 2.1 -0.21 -0.70
10/5/19 Drought-sens-canopy 182.9 95.9 -0.28 -0.71
10/5/19 Drought-sens-under 2.5 1.2 -0.32 -0.79

Diagnose your Data

# What are the properties of the data
dataset |>
  diagnose() |>
  formattable()
variables types missing_count missing_percent unique_count unique_rate
Date character 0 0 147 0.2500
Group character 0 0 4 0.0068
Sap_Flow numeric 108 18 481 0.8180
TWaterFlux numeric 0 0 508 0.8639
pLWP numeric 312 53 277 0.4711
mLWP numeric 280 48 309 0.5255
  • variables: name of each variable
  • types: data type of each variable
  • missing_count: number of missing values
  • missing_percent: percentage of missing values
  • unique_count: number of unique values
  • unique_rate: rate of unique value - unique_count / number of observations

Box Plot

Boxplot showing the IQR, lower and upper quartiles, median, and outliers

Image Credit: CÉDRIC SCHERER

Skewness

(c) Andrey Akinshin

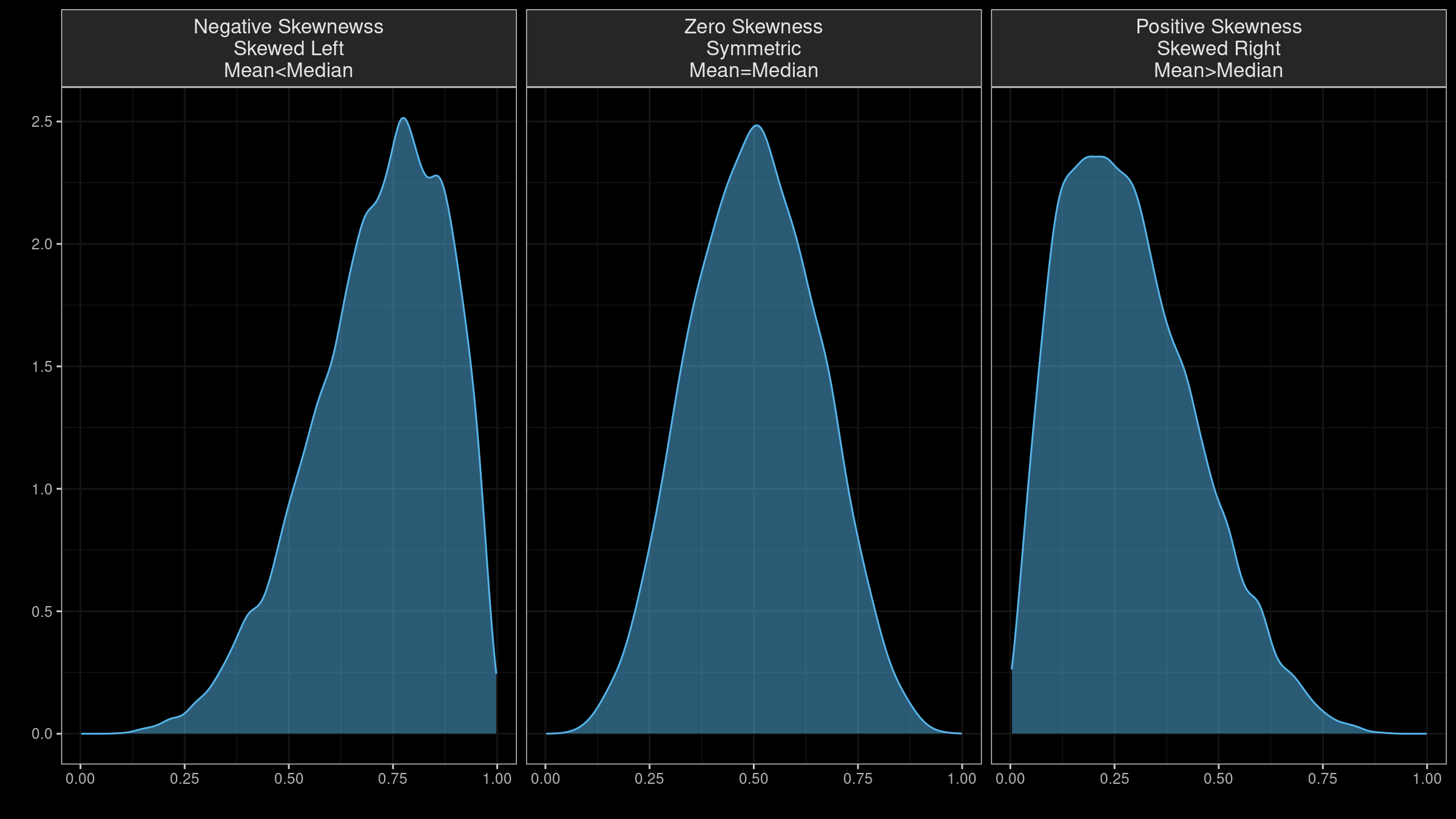
NOTE

  • “Skewness” has multiple definitions. Several underlying equations mey be at play
  • Skewness is “designed” for distributions with one peak (unimodal); it’s meaningless for distributions with multiple peaks (multimodal).
  • Most default skewness definitions are not robust: a single outlier could completely distort the skewness value.
  • We can’t make conclusions about the locations of the mean and the median based on the skewness sign.

Kurtosis

(c) Andrey Akinshin

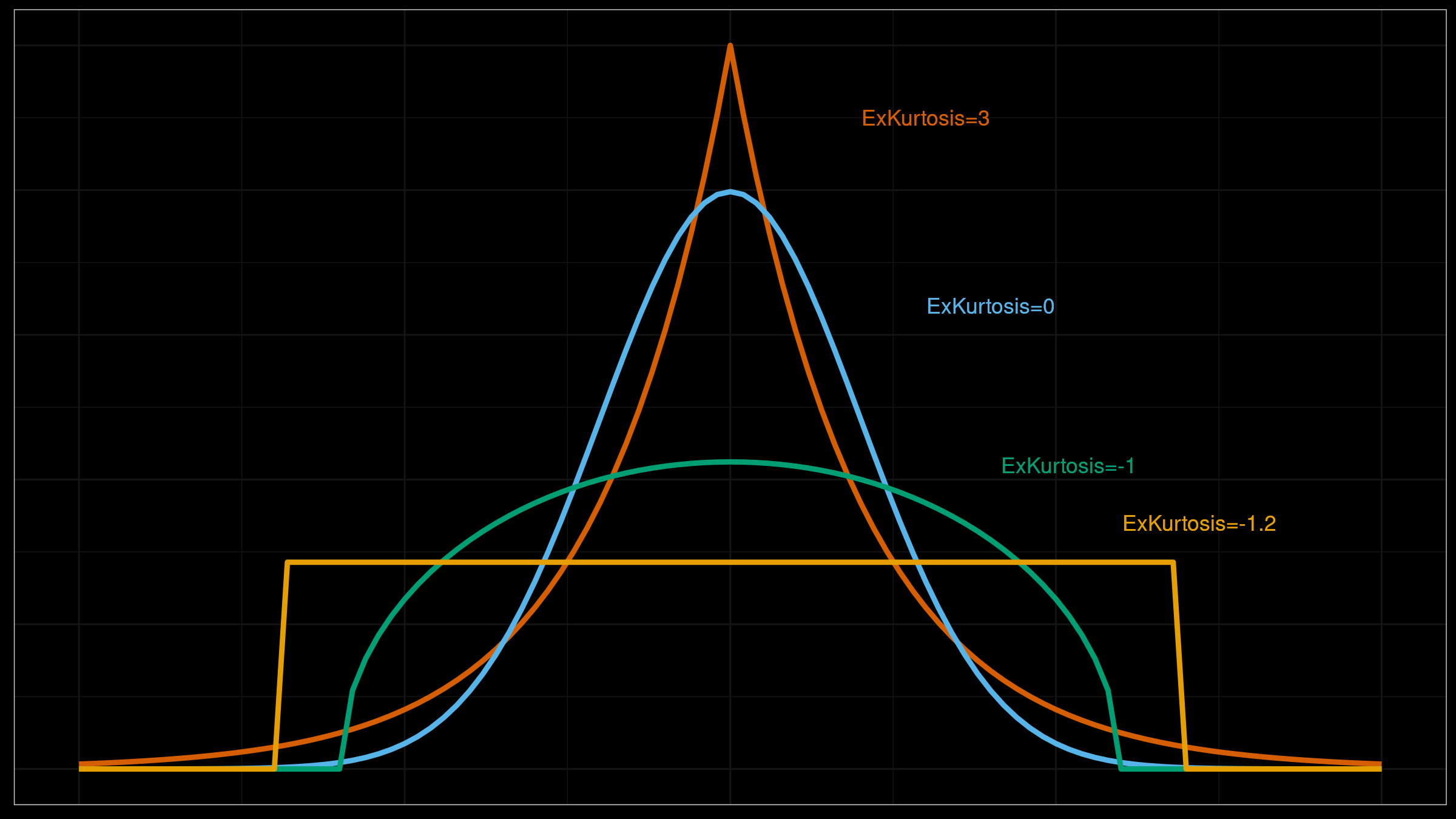
NOTE

  • There are multiple definitions of kurtosis - i.e., “kurtosis” and “excess kurtosis,” but there are other definitions of this measure.
  • Kurtosis may work fine for distributions with one peak (unimodal); it’s meaningless for distributions with multiple peaks (multimodal).
  • The classic definition of kurtosis is not robust: it could be easily spoiled by extreme outliers.

Describe your Continuous Data

# Summary statistics 
dataset |>
  describe() |>
  formattable()
described_variables n na mean sd se_mean IQR skewness kurtosis p00 p01 p05 p10 p20 p25 p30 p40 p50 p60 p70 p75 p80 p90 p95 p99 p100
Sap_Flow 480 108 25.09 40.52 1.849 13.92 2.2 4.20 0.17 0.33 0.47 1.15 2.26 2.45 3.76 5.05 5.82 9.03 10.51 16.37 48.89 83.48 109.84 176.99 184.04
TWaterFlux 588 0 11.93 19.05 0.786 6.28 2.1 3.88 0.10 0.15 0.22 0.60 1.14 1.29 1.70 2.31 3.00 4.20 5.21 7.58 23.37 43.14 51.81 80.87 96.01
pLWP 276 312 -0.61 0.23 0.014 0.26 -1.1 1.77 -1.43 -1.32 -1.07 -0.88 -0.73 -0.71 -0.68 -0.62 -0.59 -0.55 -0.49 -0.45 -0.41 -0.35 -0.30 -0.24 -0.21
mLWP 308 280 -1.03 0.30 0.017 0.42 -0.8 -0.18 -1.81 -1.79 -1.62 -1.46 -1.32 -1.23 -1.13 -1.04 -0.95 -0.90 -0.84 -0.81 -0.76 -0.71 -0.67 -0.59 -0.55
  • describes_variables: name of the column being described
  • n: number of observations excluding missing values
  • na: number of missing values
  • mean: arithmetic average
  • sd: standard deviation
  • se_mean: standard error mean. sd/sqrt(n)
  • IQR: interquartile range (Q3-Q1)
  • skewness: skewness
  • kurtosis: kurtosis
  • p25: Q1. 25% percentile
  • p50: median. 50% percentile
  • p75: Q3. 75% percentile
  • p01, p05, p10, p20, p30: 1%, 5%, 20%, 30% percentiles
  • p40, p60, p70, p80: 40%, 60%, 70%, 80% percentiles
  • p90, p95, p99, p100: 90%, 95%, 99%, 100% percentiles

Describe your Continuous Data: Refined

The above is pretty overwhelming, and most people don’t care about percentiles outside of Q1, Q3, and the median (Q2).

# Summary statistics, selecting the desired ones
dataset |>
  describe() |>
  select(described_variables, n, na, mean, sd, se_mean, IQR, skewness, kurtosis, p25, p50, p75) |>
  formattable()
described_variables n na mean sd se_mean IQR skewness kurtosis p25 p50 p75
Sap_Flow 480 108 25.09 40.52 1.849 13.92 2.2 4.20 2.45 5.82 16.37
TWaterFlux 588 0 11.93 19.05 0.786 6.28 2.1 3.88 1.29 3.00 7.58
pLWP 276 312 -0.61 0.23 0.014 0.26 -1.1 1.77 -0.71 -0.59 -0.45
mLWP 308 280 -1.03 0.30 0.017 0.42 -0.8 -0.18 -1.23 -0.95 -0.81

Describe Categorical Variables

dataset |>
  diagnose_category() |>
  formattable()
variables levels N freq ratio rank
Date 1/1/20 588 4 0.68 1
Date 1/10/20 588 4 0.68 1
Date 1/11/20 588 4 0.68 1
Date 1/12/20 588 4 0.68 1
Date 1/13/20 588 4 0.68 1
Date 1/14/20 588 4 0.68 1
Date 1/15/20 588 4 0.68 1
Date 1/16/20 588 4 0.68 1
Date 1/17/20 588 4 0.68 1
Date 1/18/20 588 4 0.68 1
Group Drought-sens-canopy 588 147 25.00 1
Group Drought-sens-under 588 147 25.00 1
Group Drought-tol-canopy 588 147 25.00 1
Group Drought-tol-under 588 147 25.00 1
  • variables: category names
  • levels: group names within categories
  • N: number of observation
  • freq: number of observation at group level / number of observation at category level
  • ratio: percentage of observation at group level / number of observation at category level
  • rank: rank of the occupancy ratio of levels (order in which the groups are in the category)

Group Descriptive Statistics

dataset |>
  group_by(Group) |>
  describe() |>
  select(described_variables, Group, n, na, mean, sd, se_mean, IQR, skewness, kurtosis, p25, p50, p75) |>
  formattable()
described_variables Group n na mean sd se_mean IQR skewness kurtosis p25 p50 p75
Sap_Flow Drought-sens-canopy 120 27 85.27 41.314 3.771 40.09 1.0493 0.150 53.98 76.72 94.07
Sap_Flow Drought-sens-under 120 27 1.45 0.804 0.073 1.66 -0.2242 -1.635 0.53 1.67 2.19
Sap_Flow Drought-tol-canopy 120 27 9.07 1.396 0.127 2.28 -0.6344 -0.695 8.12 9.29 10.40
Sap_Flow Drought-tol-under 120 27 4.57 0.902 0.082 1.09 -0.9141 -0.077 4.05 4.94 5.14
TWaterFlux Drought-sens-canopy 147 0 40.40 19.028 1.569 24.88 0.9210 0.509 25.22 38.63 50.10
TWaterFlux Drought-sens-under 147 0 0.75 0.429 0.035 0.84 0.0105 -1.188 0.27 0.82 1.11
TWaterFlux Drought-tol-canopy 147 0 4.36 0.940 0.078 1.51 -0.3548 -0.940 3.60 4.46 5.11
TWaterFlux Drought-tol-under 147 0 2.19 0.598 0.049 0.95 -0.0087 -0.779 1.74 2.20 2.69
mLWP Drought-sens-canopy 77 70 -1.32 0.298 0.034 0.41 0.3178 -0.691 -1.53 -1.35 -1.11
mLWP Drought-sens-under 77 70 -1.10 0.264 0.030 0.43 -0.3411 -0.313 -1.34 -1.05 -0.91
mLWP Drought-tol-canopy 77 70 -0.89 0.092 0.010 0.12 -0.2608 -0.402 -0.95 -0.89 -0.83
mLWP Drought-tol-under 77 70 -0.81 0.171 0.019 0.21 -0.9539 -0.412 -0.91 -0.74 -0.70
pLWP Drought-sens-canopy 69 78 -0.67 0.246 0.030 0.32 -0.3510 -0.274 -0.79 -0.71 -0.47
pLWP Drought-sens-under 69 78 -0.70 0.284 0.034 0.28 -1.1510 0.480 -0.80 -0.59 -0.52
pLWP Drought-tol-canopy 69 78 -0.63 0.096 0.012 0.14 -0.4644 -0.592 -0.71 -0.60 -0.57
pLWP Drought-tol-under 69 78 -0.44 0.132 0.016 0.16 -0.4333 -0.432 -0.52 -0.41 -0.36

Testing Normality

  • Shapiro-Wilk test & Q-Q plots
  • Testing overall normality of two columns
  • Testing normality of groups

Normality of Columns

Shapiro-Wilk Test

Shapiro-Wilk test looks at whether a target distribution is sample form a normal distribution

dataset |>
  normality() |>
  formattable()
vars statistic p_value sample
Sap_Flow 0.63 7.4e-31 588
TWaterFlux 0.64 2.2e-33 588
pLWP 0.93 3.4e-10 588
mLWP 0.93 7.0e-11 588

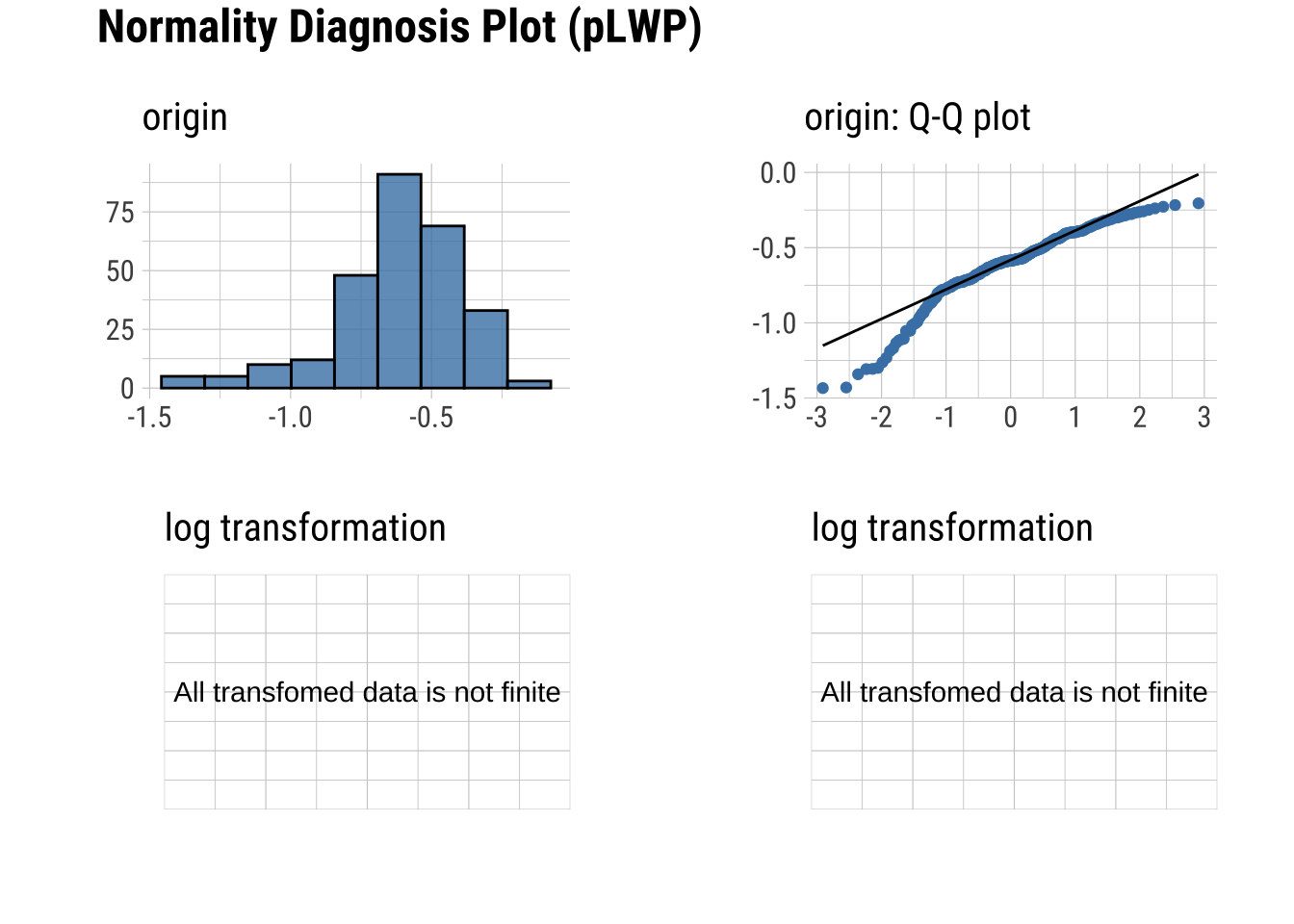
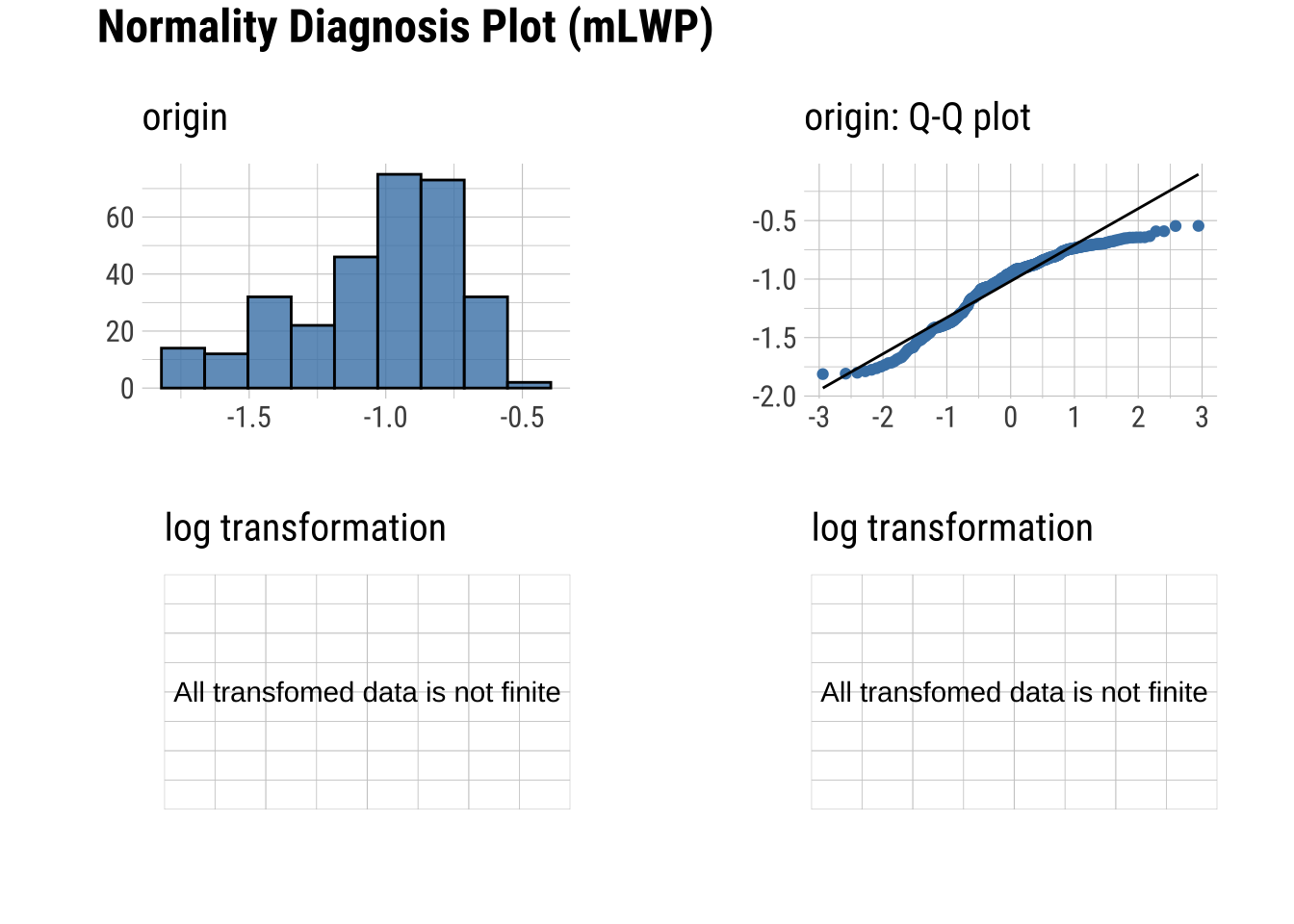
Q-Q Plots

Plots of the quartiles of a target data set and plot it against predicted quartiles from a normal distribution

dataset |>
plot_normality()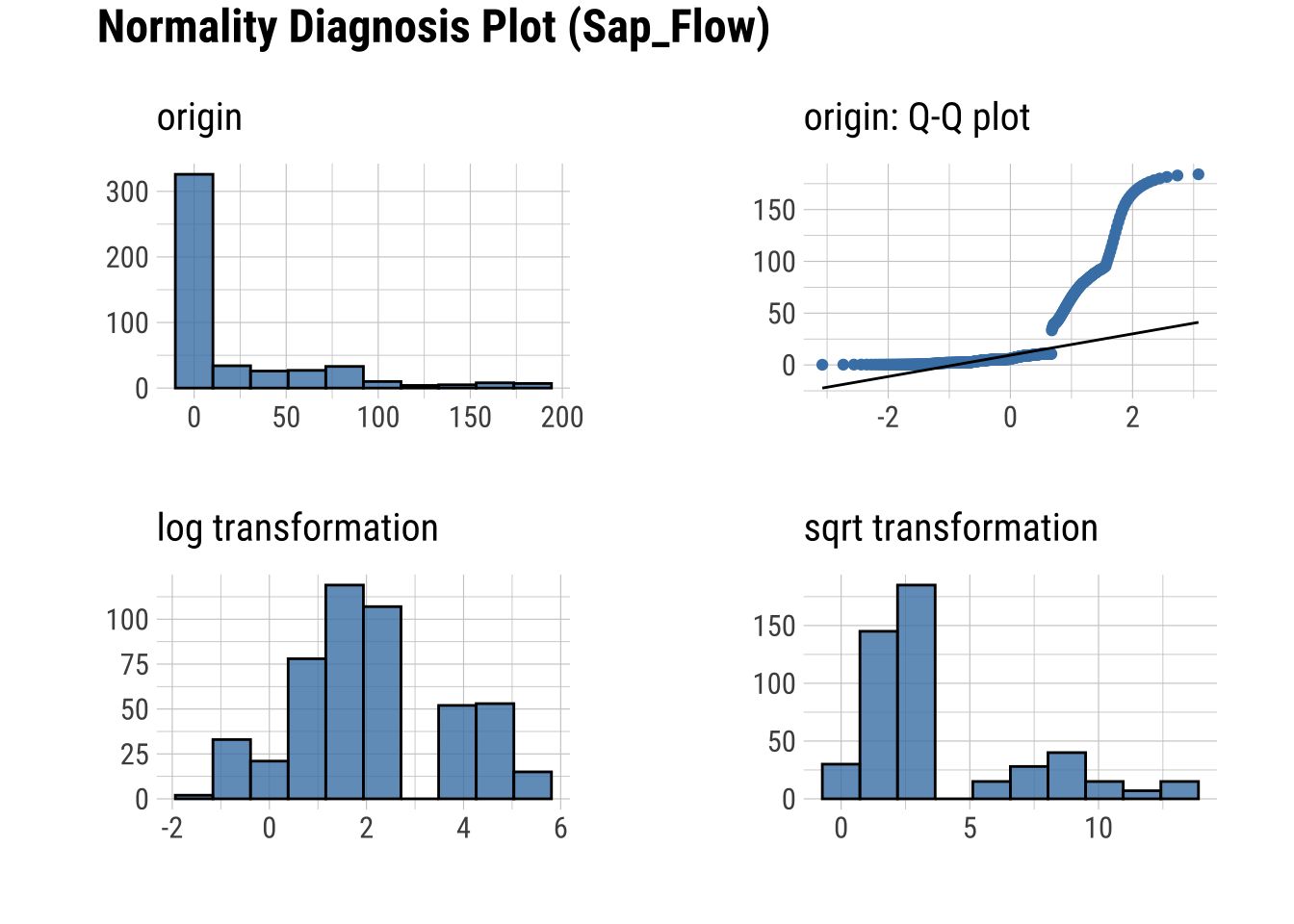

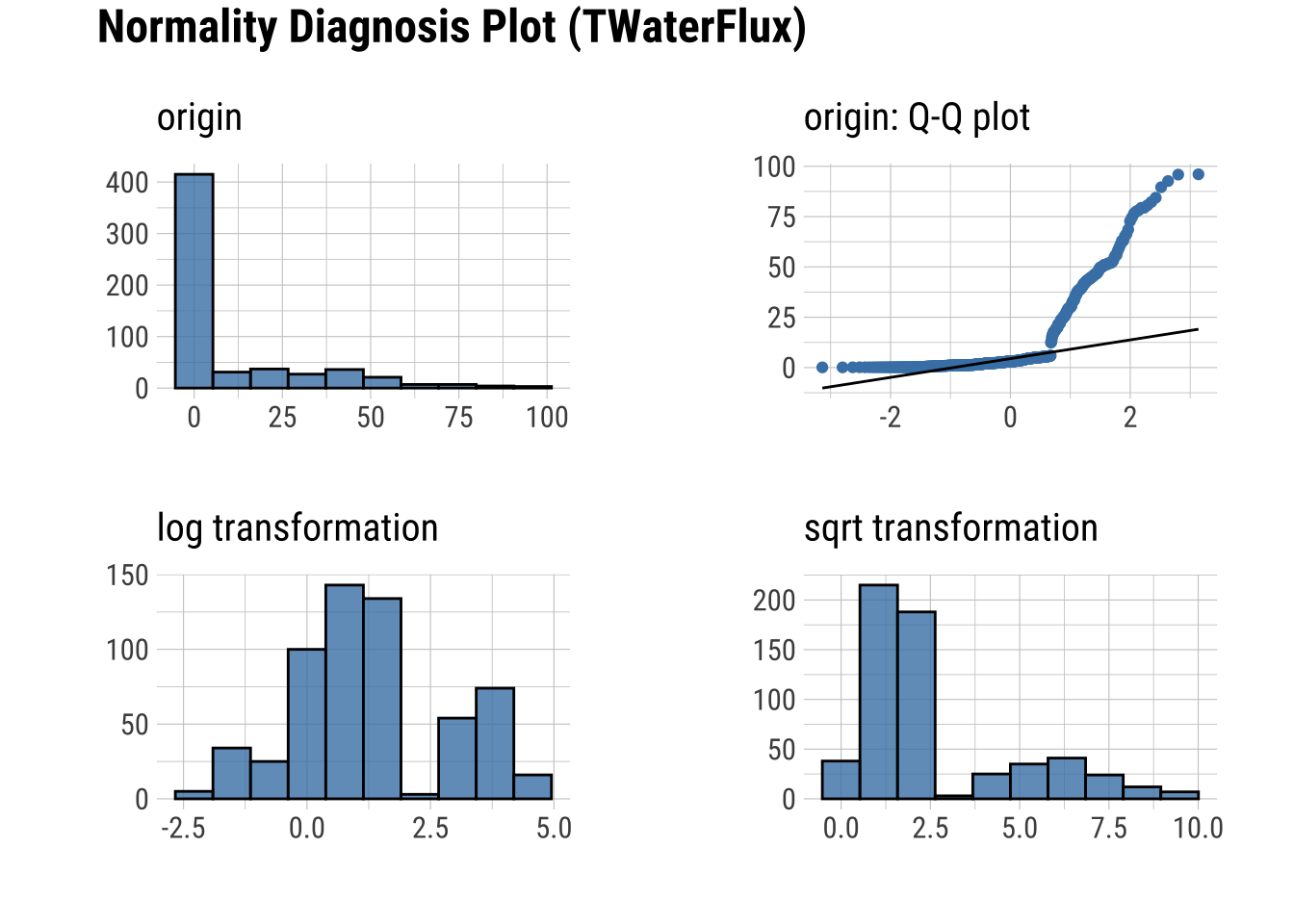
Normality within Groups

Looking within Age_group at the subgroup normality

Shapiro-Wilk Test

dataset |>
  group_by(Group) |>
  select(Sap_Flow, TWaterFlux, Group) |>
  normality() |>
  formattable()
variable Group statistic p_value sample
Sap_Flow Drought-sens-canopy 0.87 9.8e-09 147
Sap_Flow Drought-sens-under 0.86 2.2e-09 147
Sap_Flow Drought-tol-canopy 0.91 8.3e-07 147
Sap_Flow Drought-tol-under 0.90 2.2e-07 147
TWaterFlux Drought-sens-canopy 0.93 1.1e-06 147
TWaterFlux Drought-sens-under 0.93 1.3e-06 147
TWaterFlux Drought-tol-canopy 0.96 1.3e-04 147
TWaterFlux Drought-tol-under 0.98 4.4e-02 147

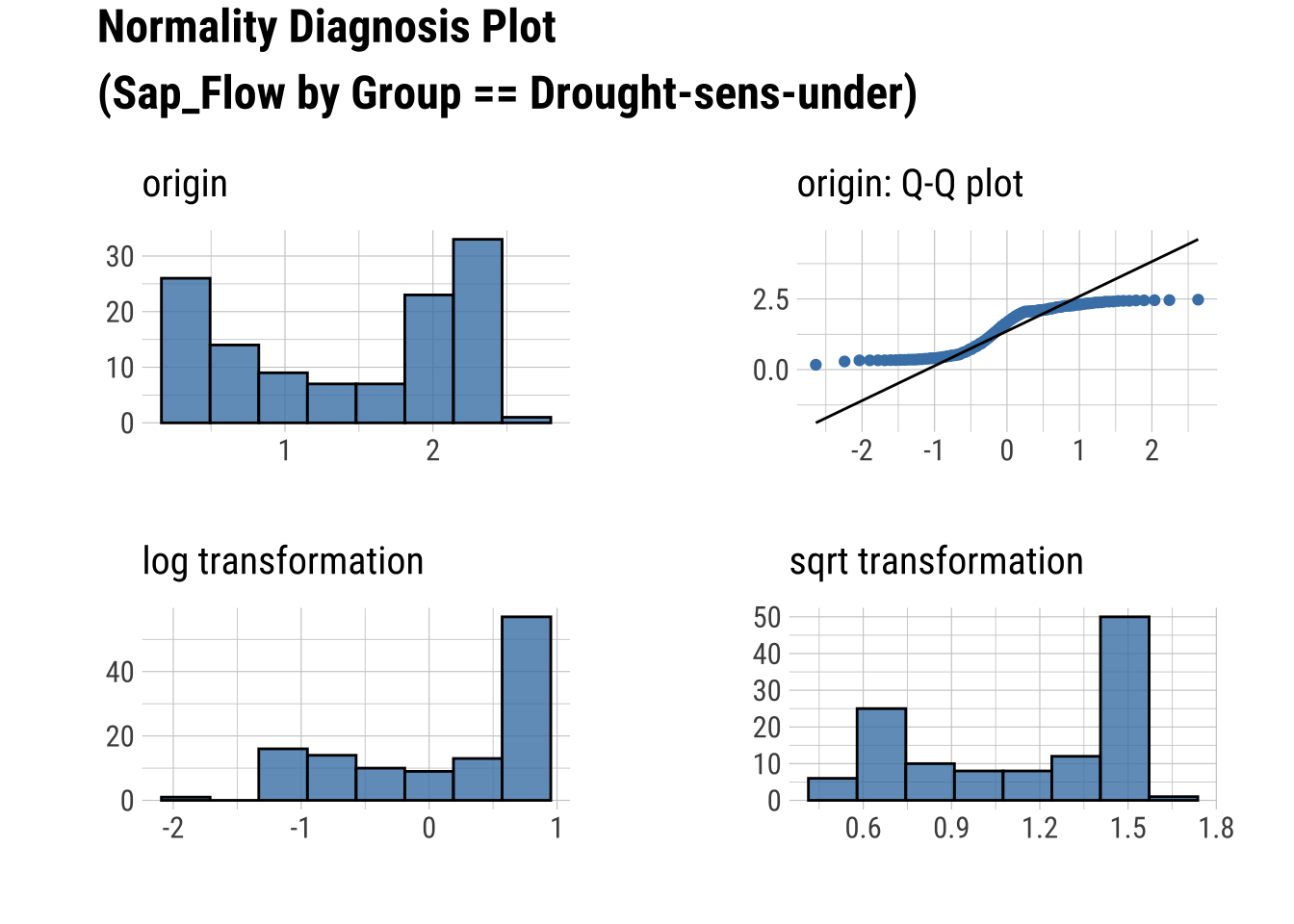
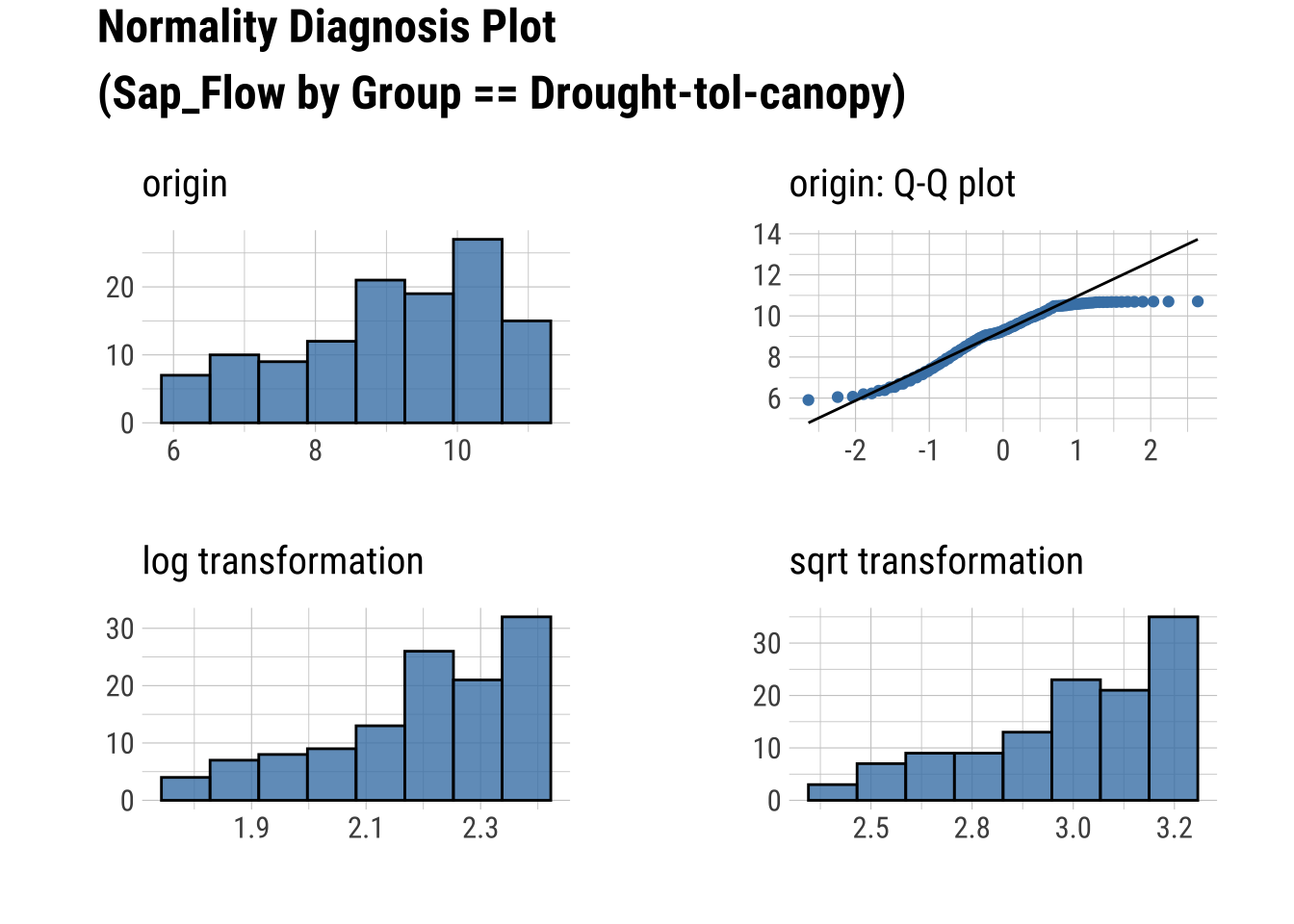
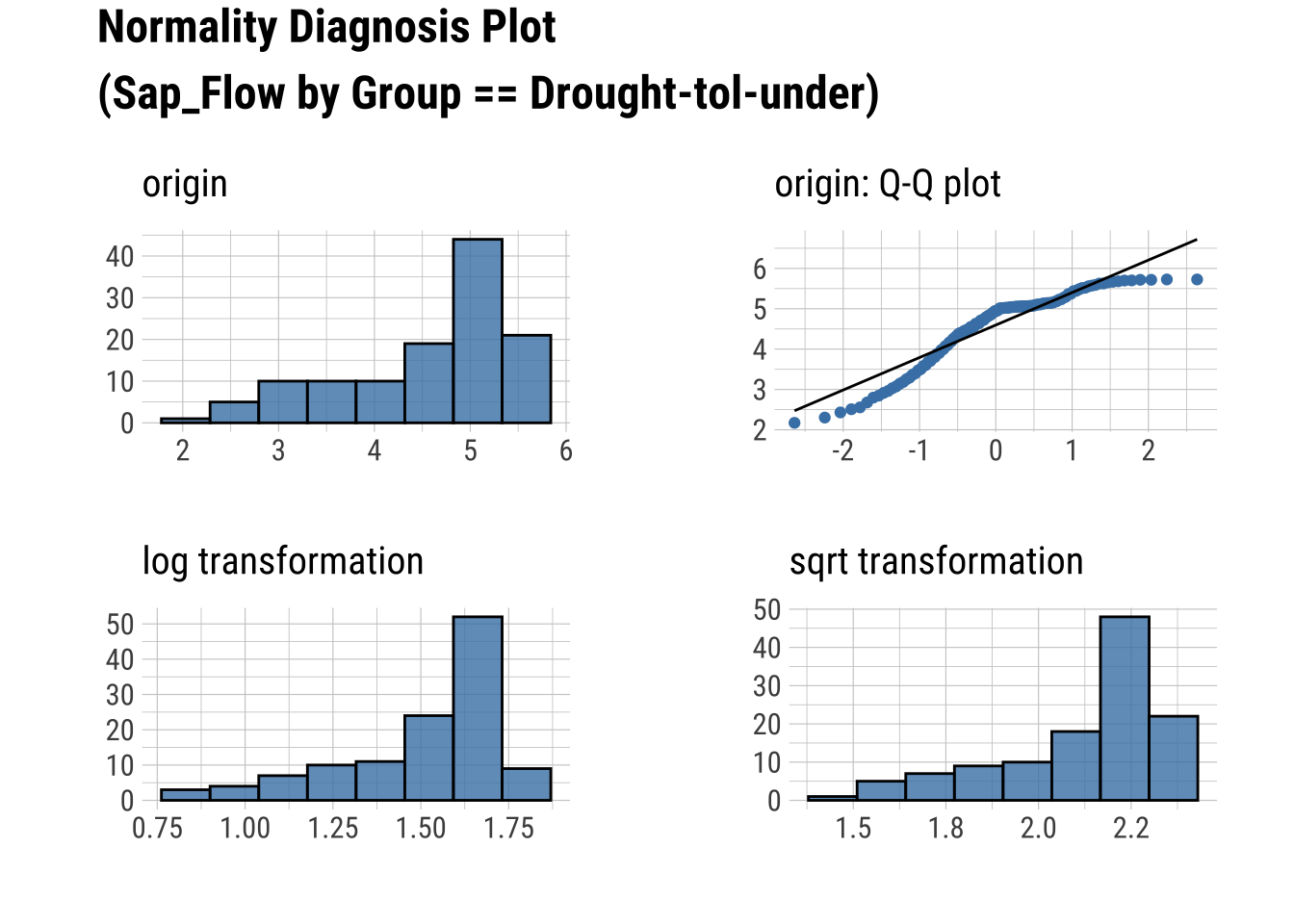
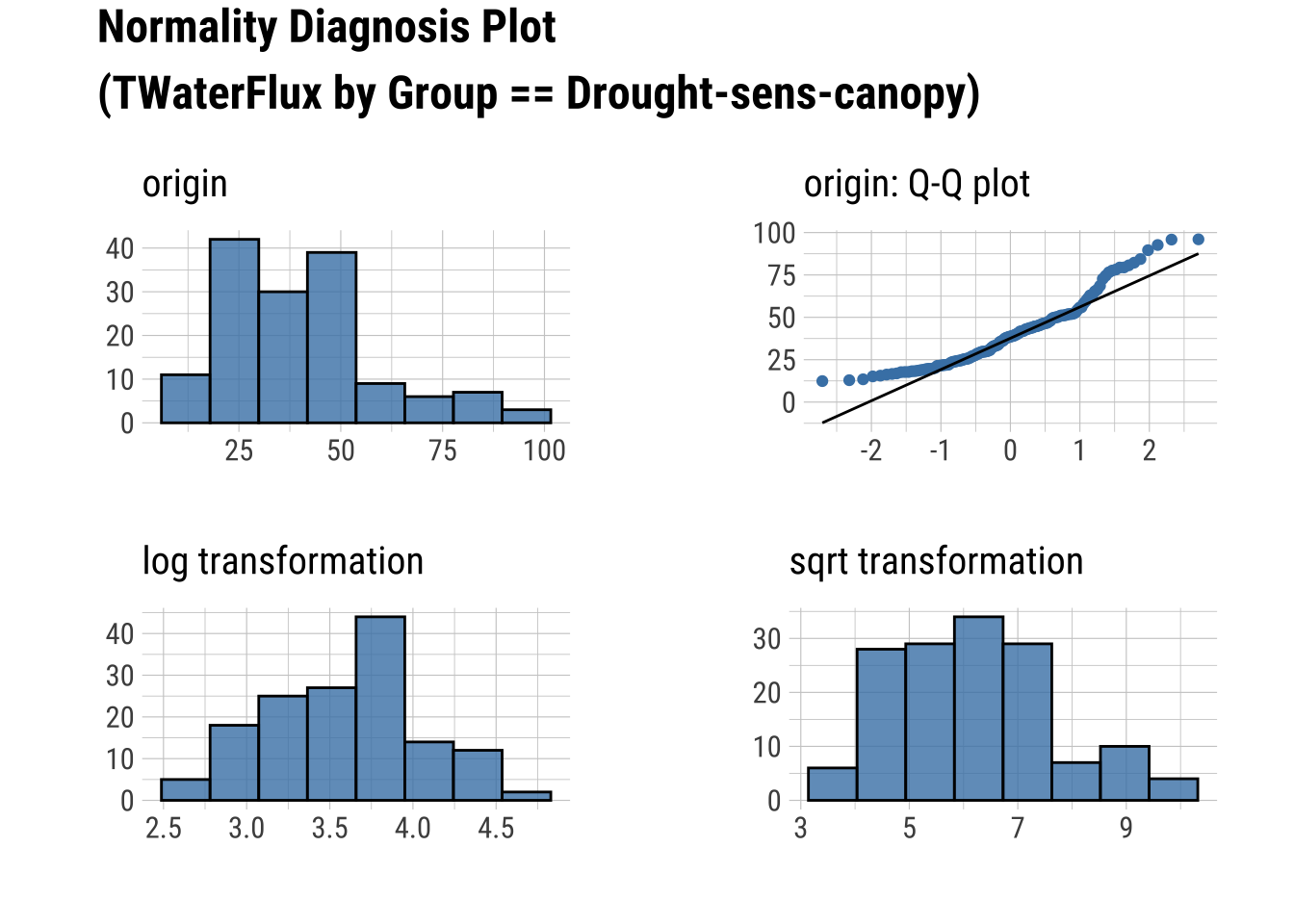
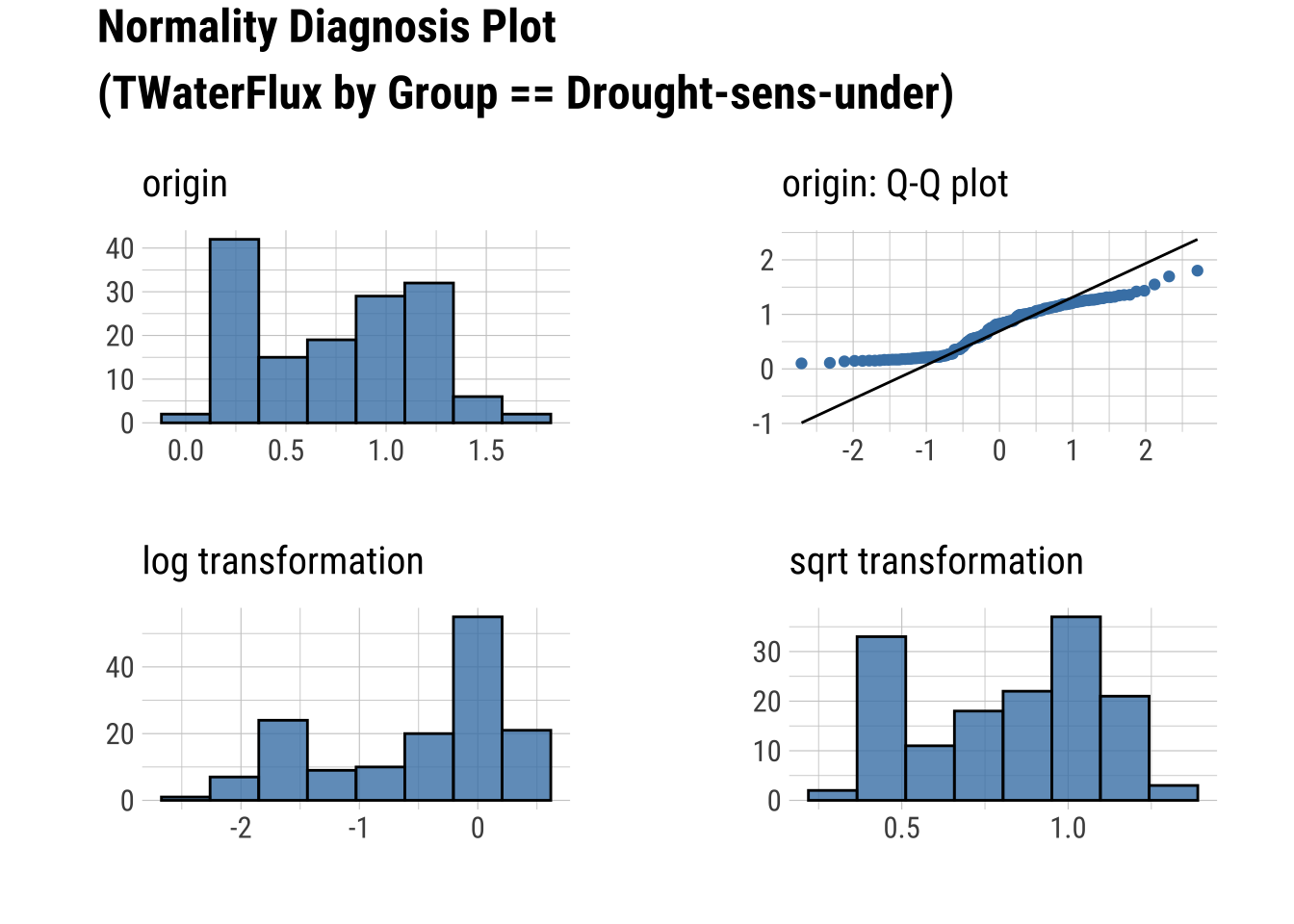
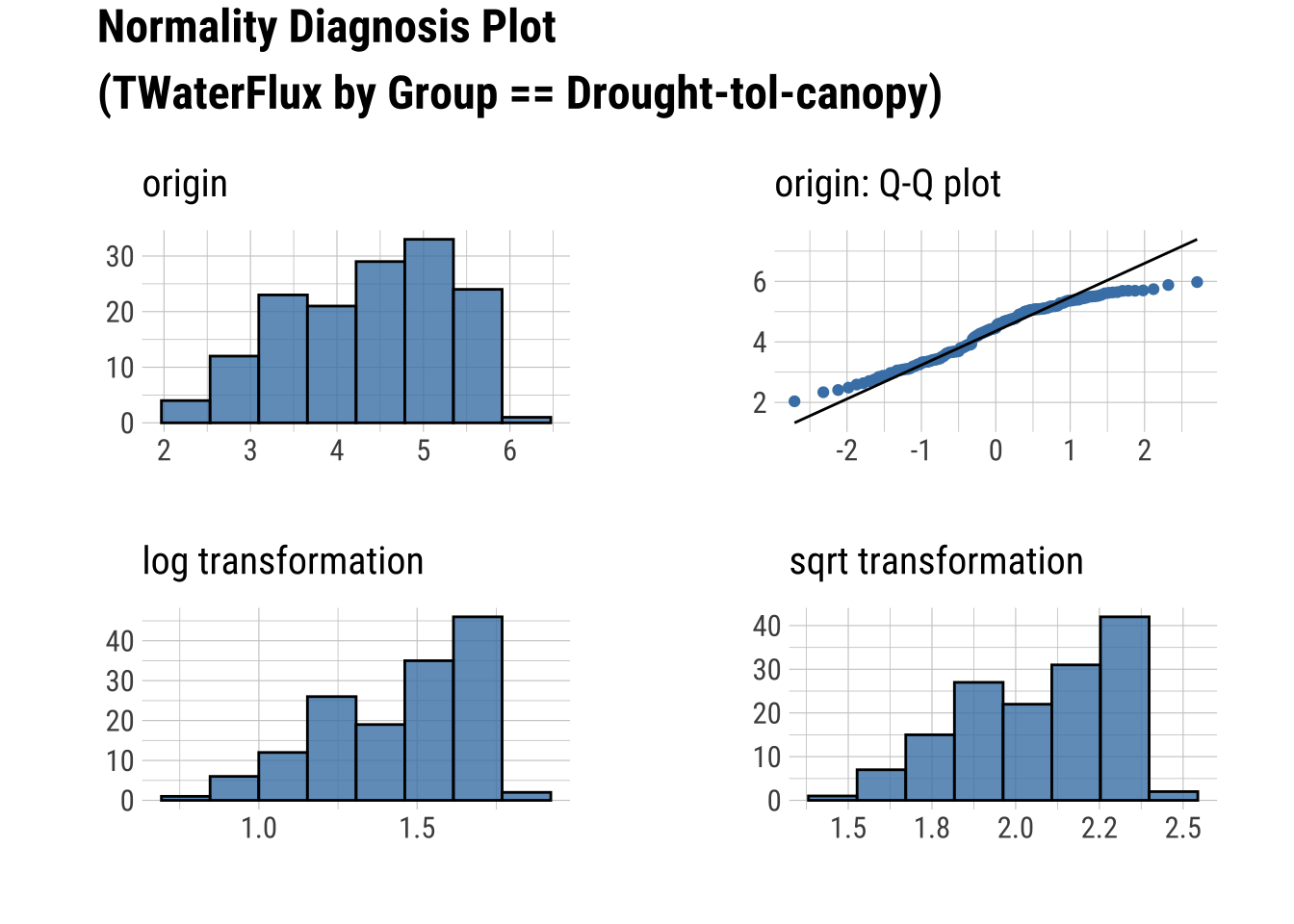
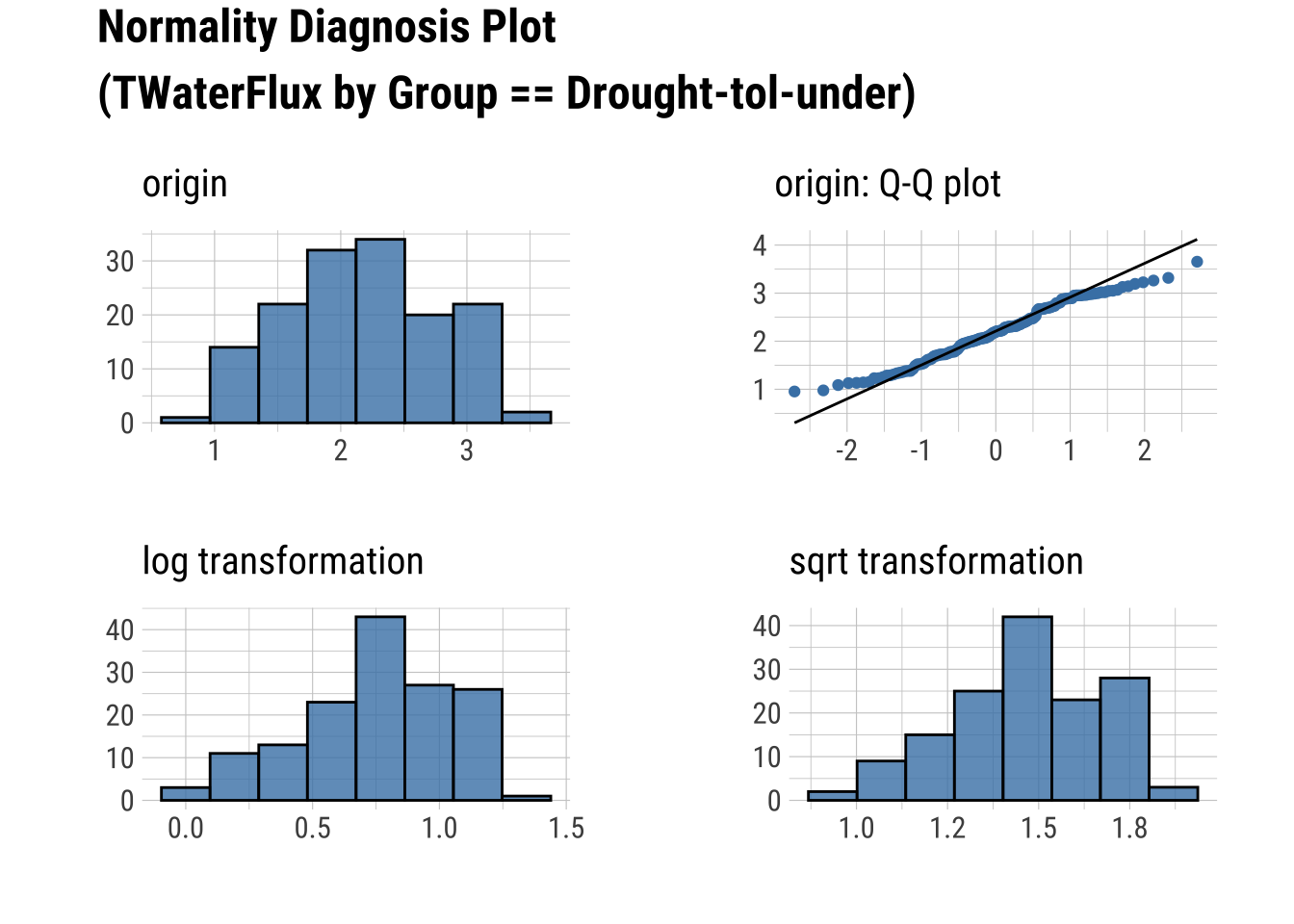
Q-Q Plots

dataset |>
group_by(Group) |>
  select(Sap_Flow, TWaterFlux, Group) |>
  plot_normality()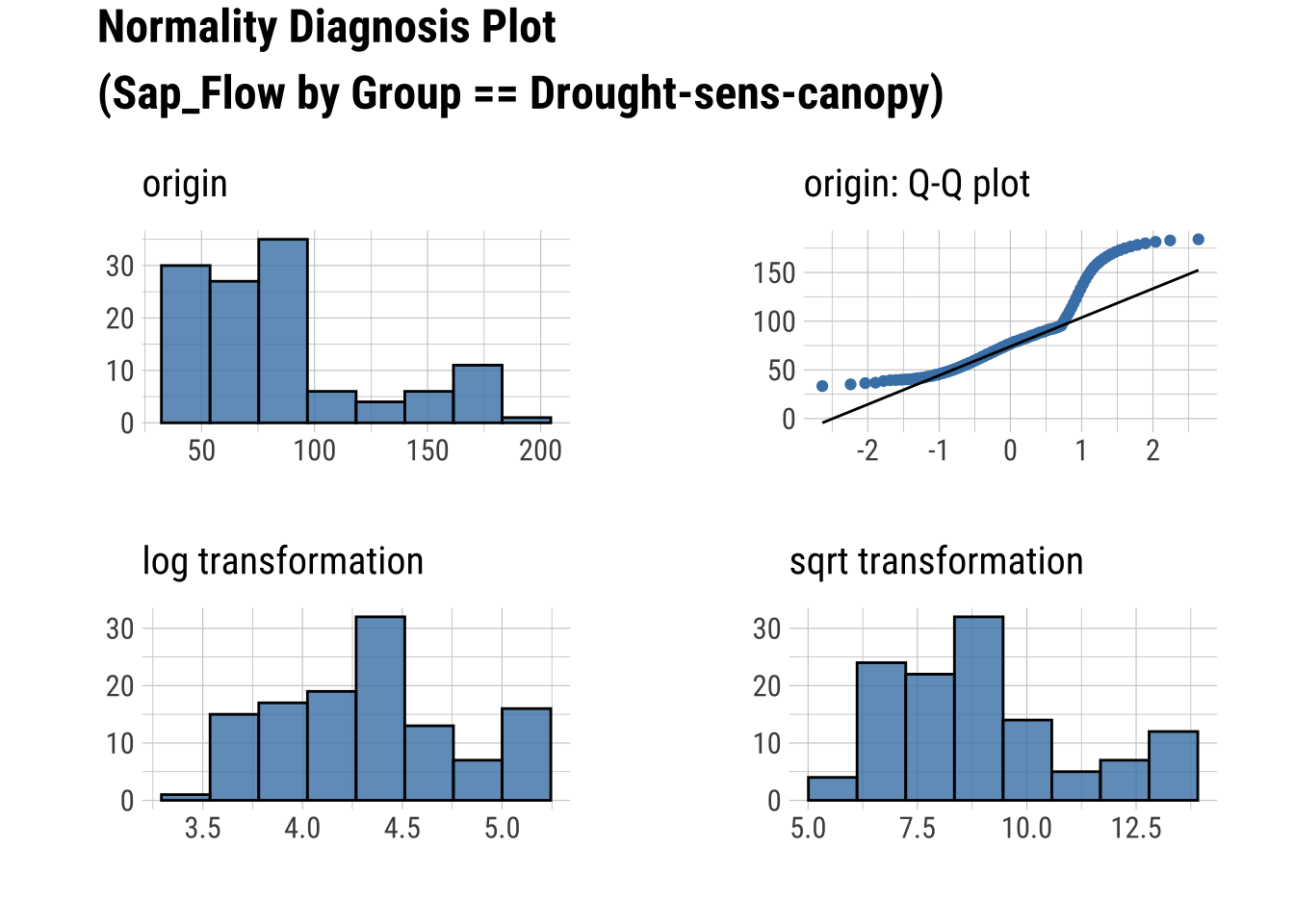

Produce an HTML Normality Summary

eda_web_report(dataset)
Meredith, Laura, S. Nemiah Ladd, and Christiane Werner. 2021. “Data for "Ecosystem Fluxes During Drought and Recovery in an Experimental Forest".” University of Arizona Research Data Repository. https://doi.org/10.25422/AZU.DATA.14632593.V1.