Introduction

(Team 2022)

Exploratory data analysis is an essential first step towards determining the validity of your data and should be performed throughout the data pipeline. However, EDA is often performed too late or not at all. The [Python programming language](https://en.wikipedia.org/wiki/Python_(programming_language), is a widely used open source platform for data analysis and data visualization. This is because of the variety of libraries available and attentive community devoted to data analysis.

Here, we utilize the pandas and pandas-profiling libraries to conduct preliminary exploratory data analysis aimed at diagnosing any major issues with an imported data set. pandas and pandas-profiling offers a clean and straightforward methodology to uncover issues such as data outliers, missing data, as well as summary statistical reports.

What is Exploratory Data Analysis?

Exploratory data analysis is a statistical, approach towards analyzing data sets to investigate and summarize their main characteristics, often through statistical graphics and other data visualization methods.

What are Some Important Data Set Characteristics?

There are several characteristics that are arguably important, but we will only consider those covered in this workshop series. Let’s start with the fundamentals that will help guide us.

Diagnostics

When importing data sets, it is important to consider characteristics about the data columns, rows, and individual cells.

Variables

Name of each variable

   Pregnancies  Glucose  BloodPressure  ...  Age  Outcome  Age_group
0            6      148             72  ...   50        1     Middle
1            1       85             66  ...   31        0     Middle
2            8      183             64  ...   32        1     Middle
3            1       89             66  ...   21        0      Young
4            0      137             40  ...   33        1     Middle

[5 rows x 10 columns]

Types

Data type of each variable

Pregnancies                   int64
Glucose                       int64
BloodPressure                 int64
SkinThickness                 int64
Insulin                       int64
BMI                         float64
DiabetesPedigreeFunction    float64
Age                           int64
Outcome                       int64
Age_group                    object
dtype: object

Numerical: Continuous

Measurable numbers that are fractional or decimal and cannot be counted (e.g., time, height, weight)

Numerical: Discrete

Countable whole numbers or integers (e.g., number of successes or failures)

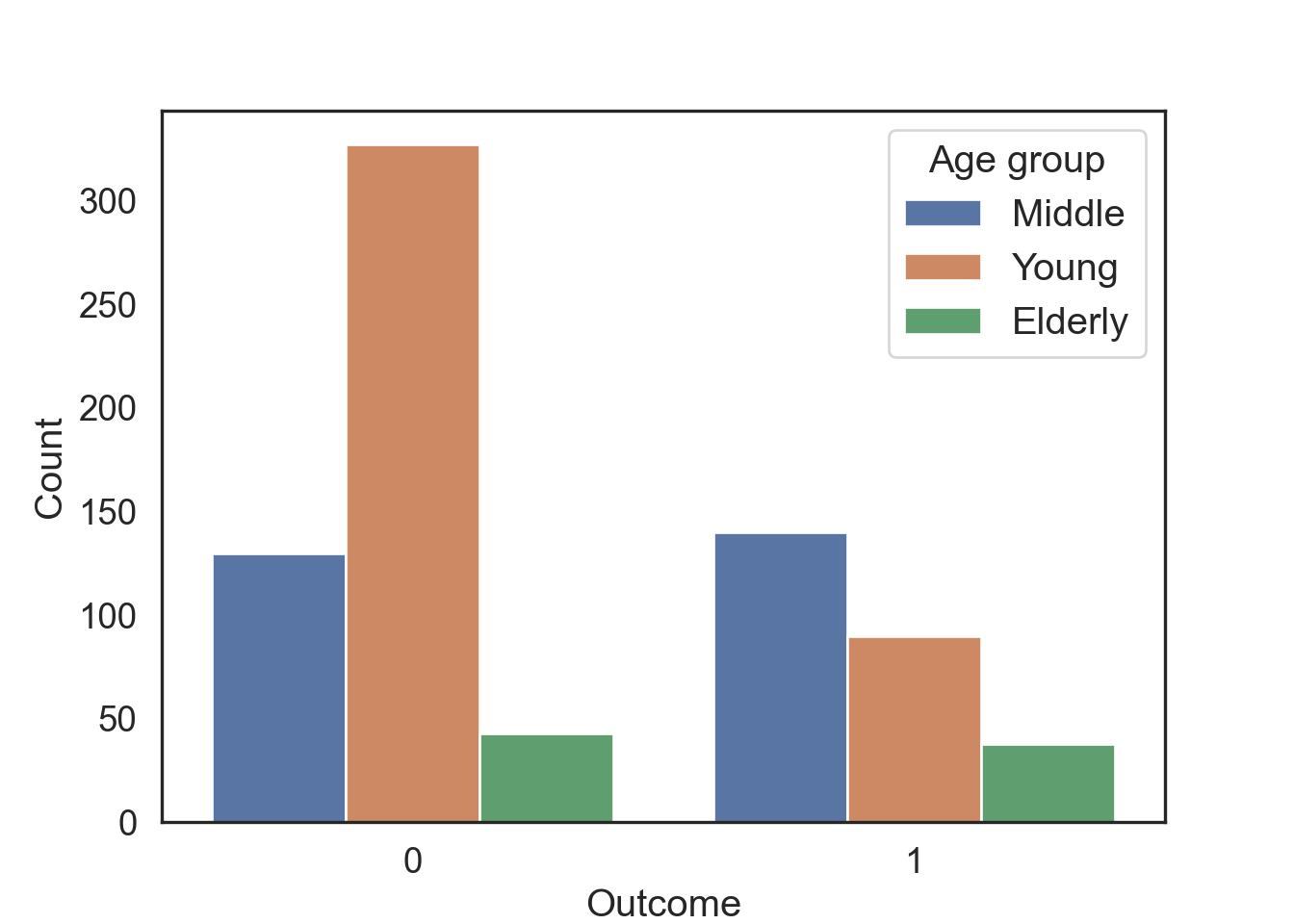
Categorical: Nominal

Labeling variables without any order or quantitative value (e.g., hair color, nationality)

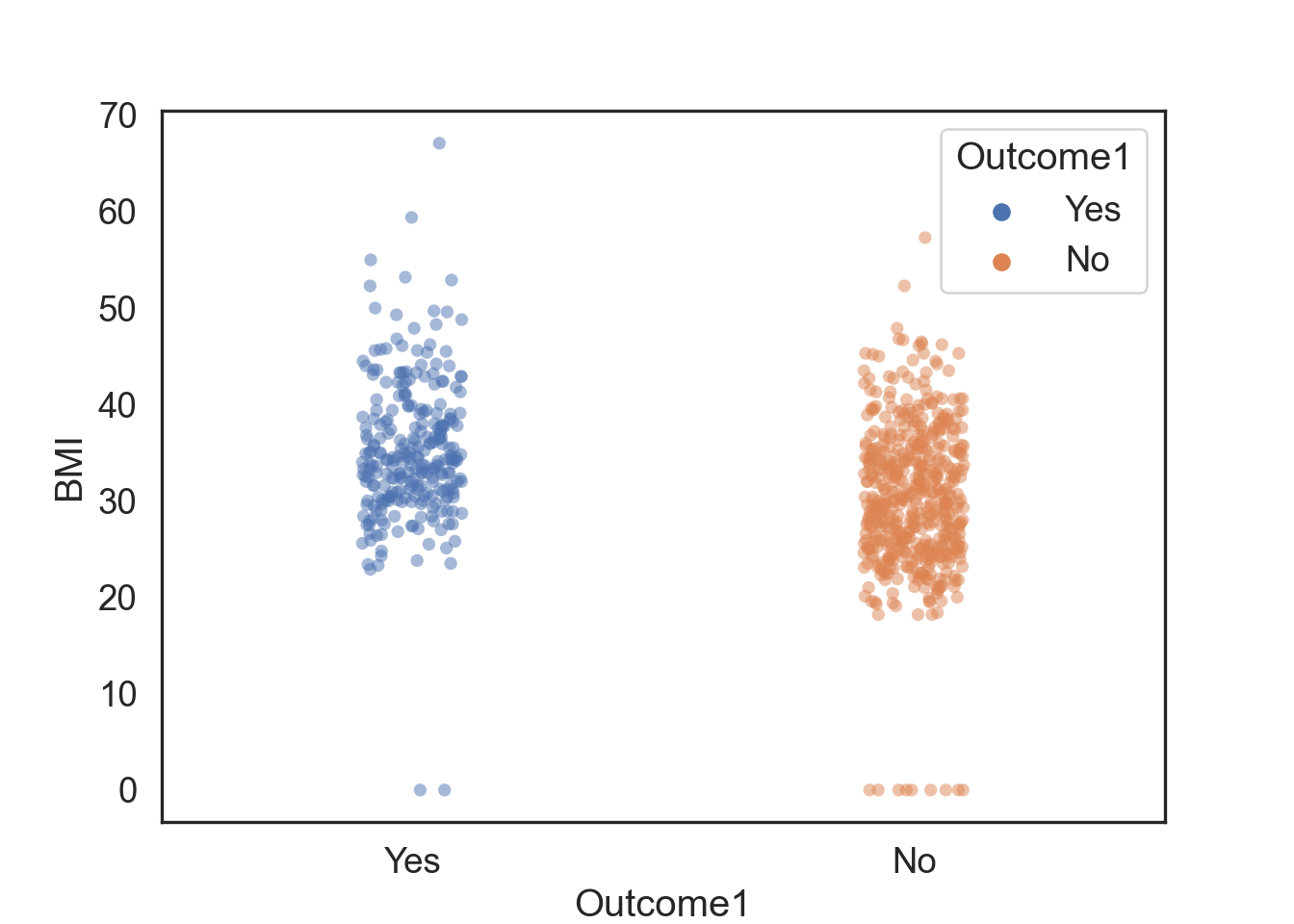
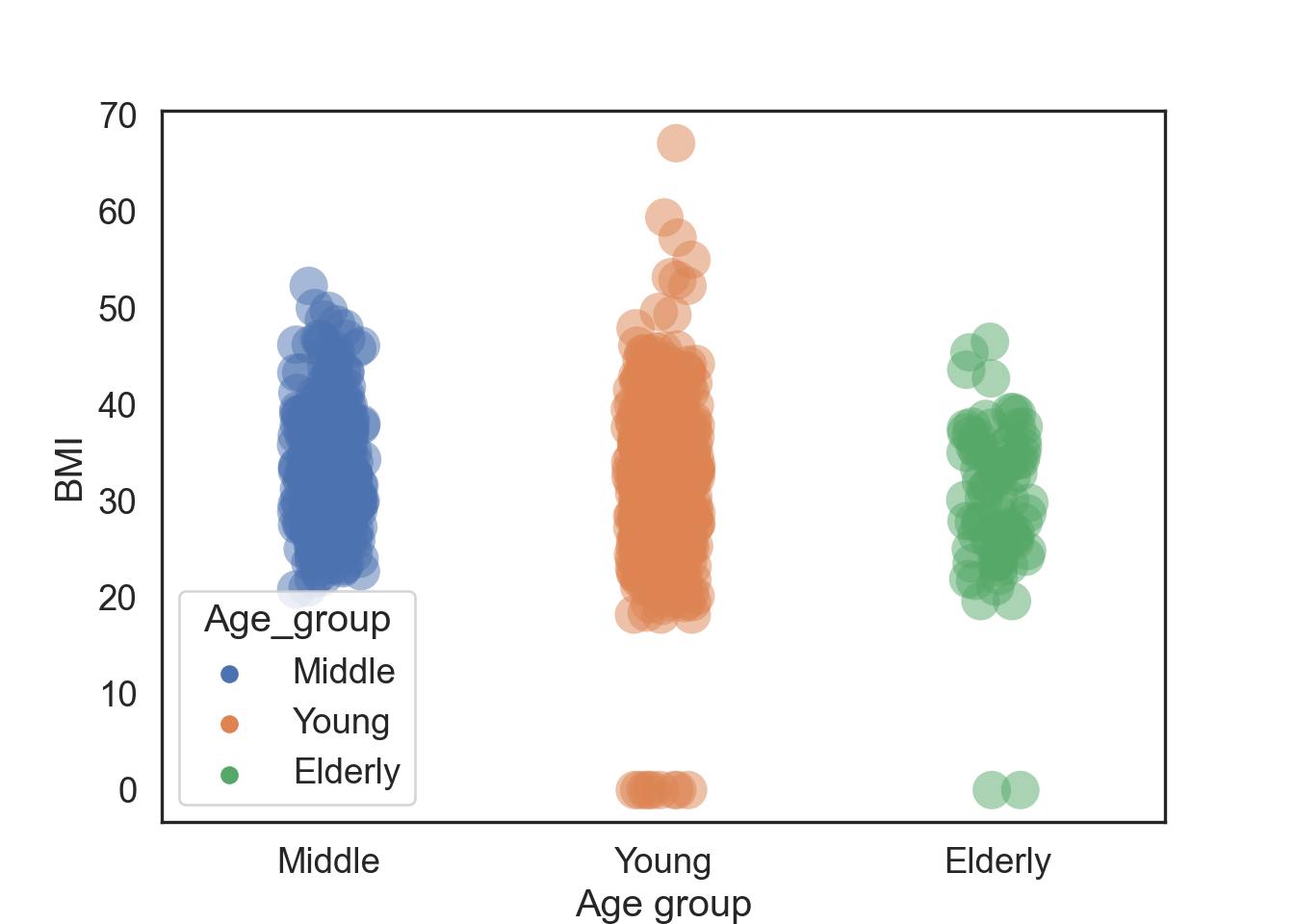
Categorical: Ordinal

Where there is a hierarchical order along a scale (e.g., ranks, letter grades, age groups)

Missing Values (NAs)

Cells, rows, or columns without data

  • Missing percent: percentage of missing values * Unique count: number of unique values.

  • Unique rate: rate of unique value - unique count / total number of observations.

   Pregnancies  Glucose  BloodPressure  ...  Outcome  Age_group  Outcome1
0          6.0    148.0           72.0  ...      1.0     Middle       NaN
1          1.0     85.0           66.0  ...      0.0     Middle        No
2          8.0    183.0           64.0  ...      1.0     Middle       Yes
3          1.0     89.0           66.0  ...      0.0      Young        No
4          NaN    137.0           40.0  ...      1.0     Middle       Yes

[5 rows x 11 columns]

Summary Statistics

Above we described some properties of data. However, you will need to know some descriptive characteristics of your data before you can move forward. Enter, summary statistics.

Summary statistics allow you to summarize large amounts of information about your data as quickly as possible.

Central Tendency

Measuring a central property of your data. Some examples you’ve probably heard of are:

  • Mean: Average value

  • Median: Middle value

  • Mode: Most common value

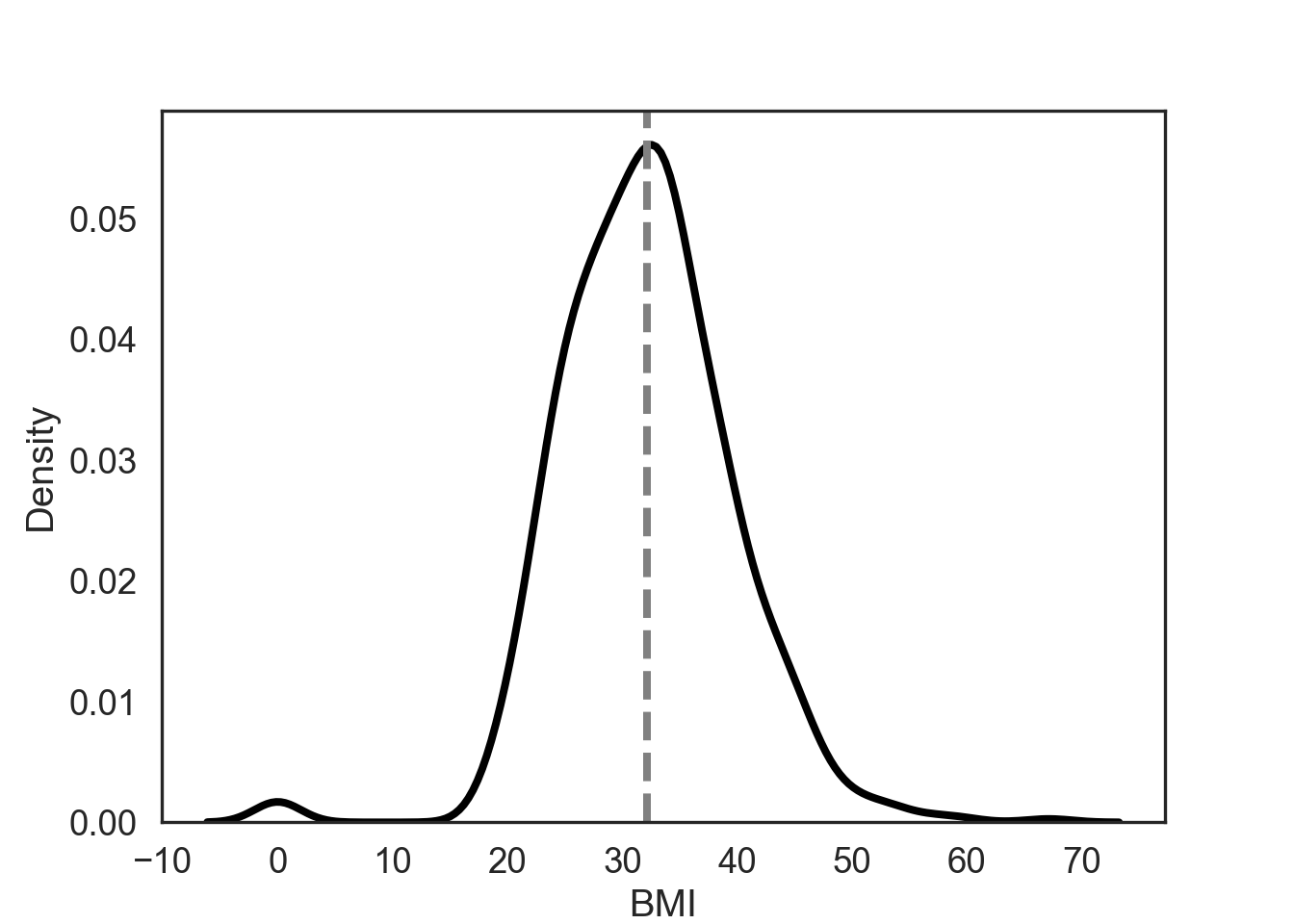
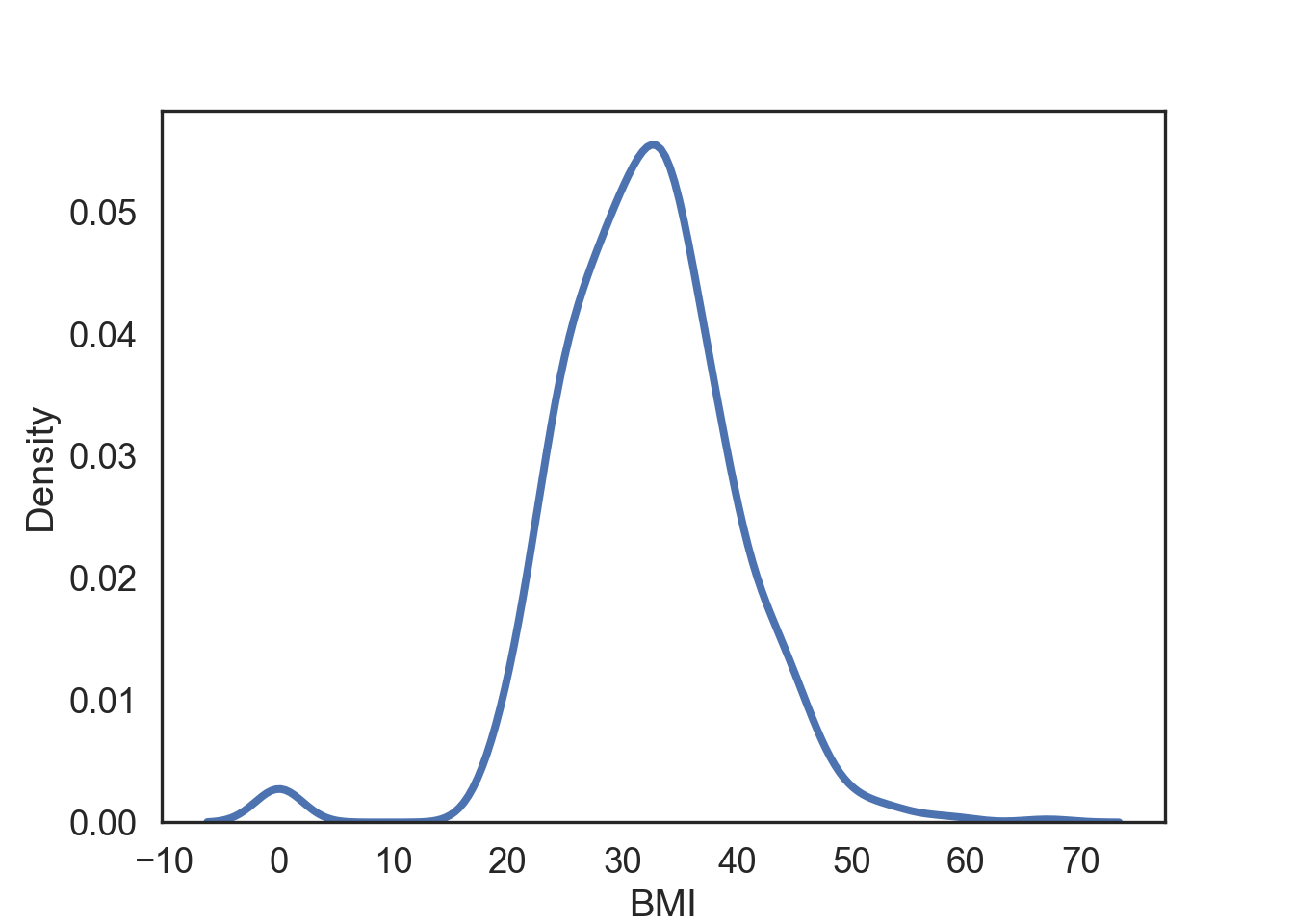
Notice that all values of central tendency can be pretty similar in this figure.

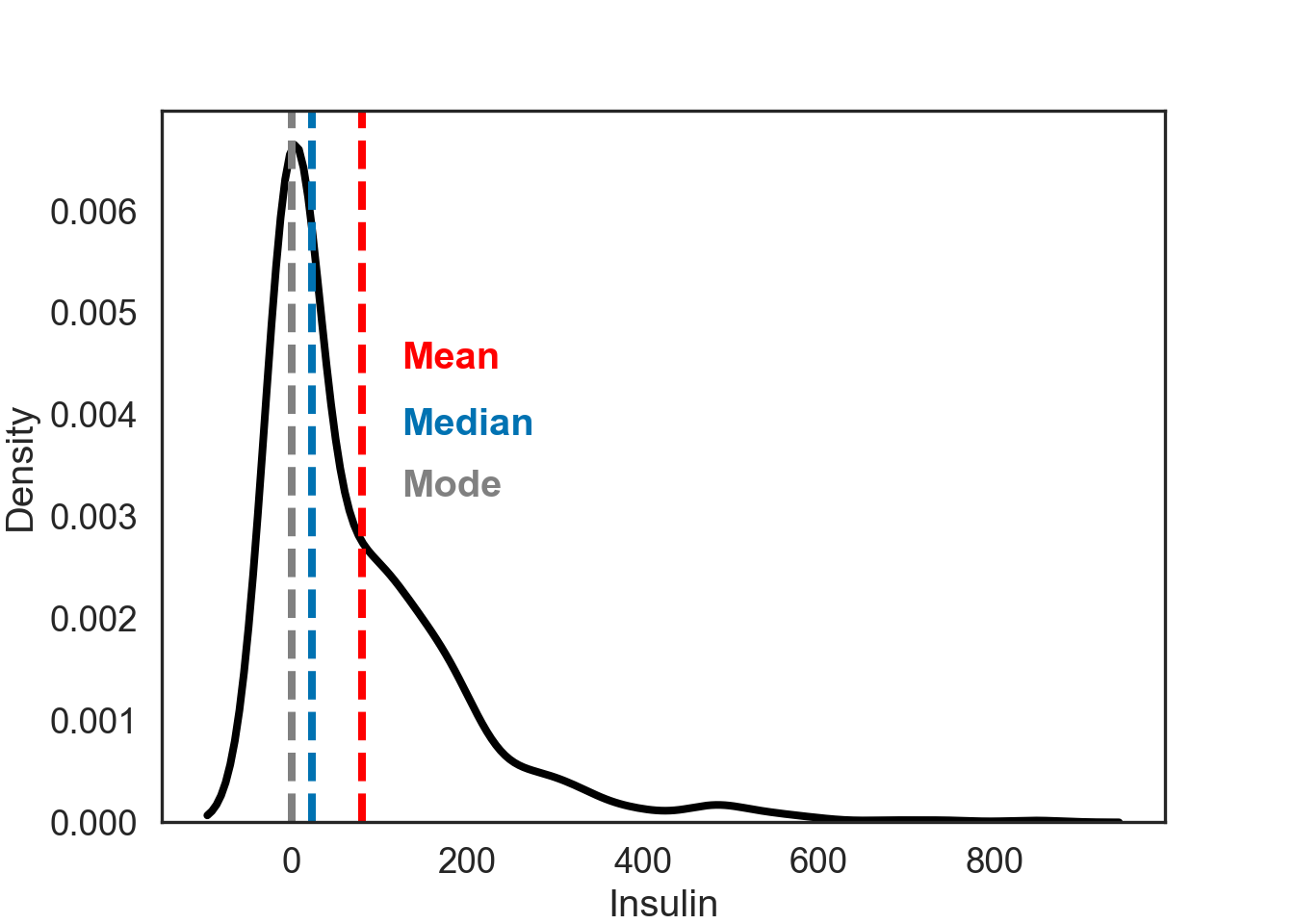
However, in this figure, all measures are different. This will be important when we discuss statistical dispersion in chapter 3.

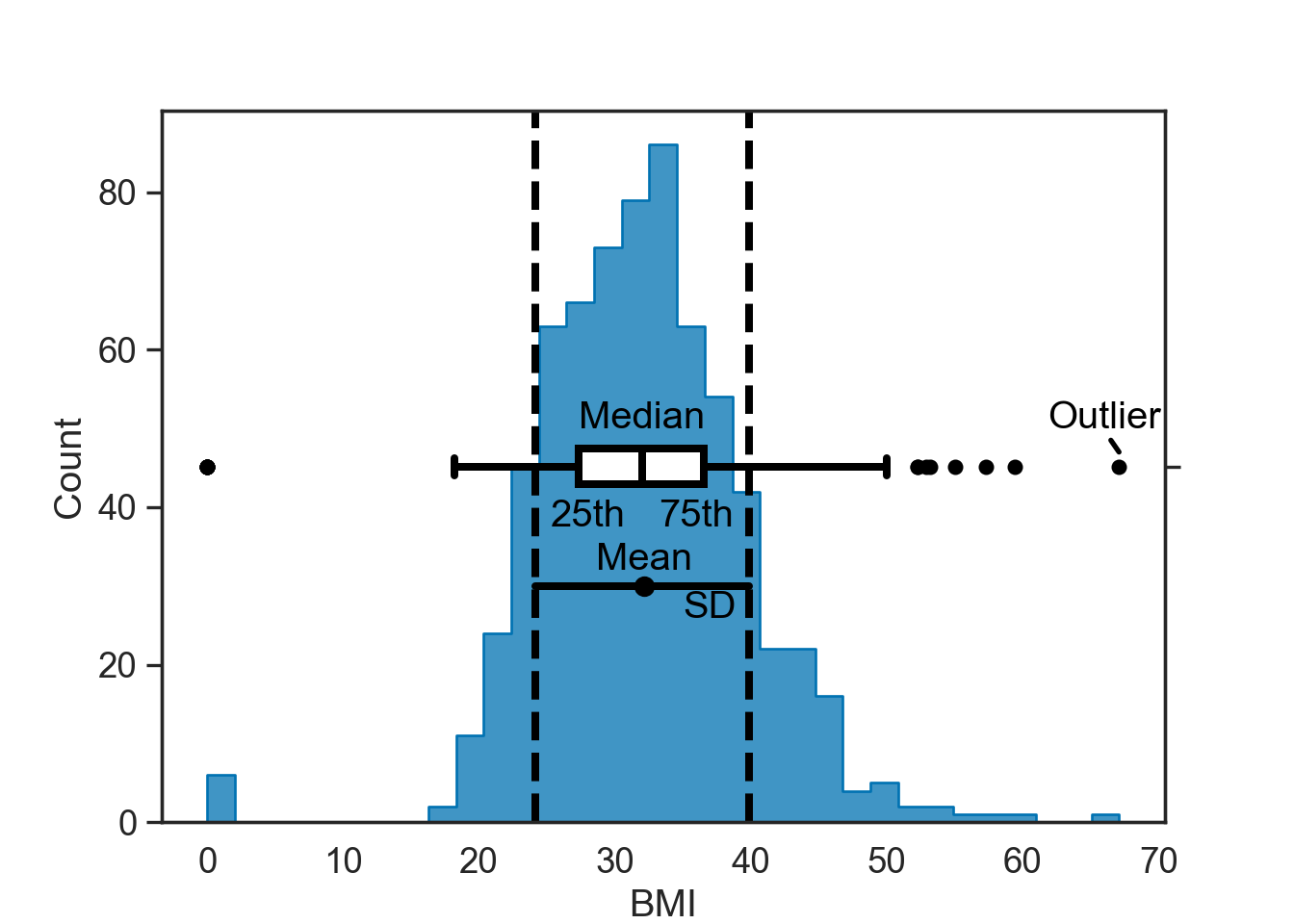
Statistical Dispersion

Measure of data variability, scatter, or spread. Some examples you may have heard of:

  • Standard deviation (SD): The amount of variation that occurs in a set of values.

  • Interquartile range (IQR): The difference between the 75th and 25th percentiles

  • Outliers: A value outside of \(1.5 * IQR\)

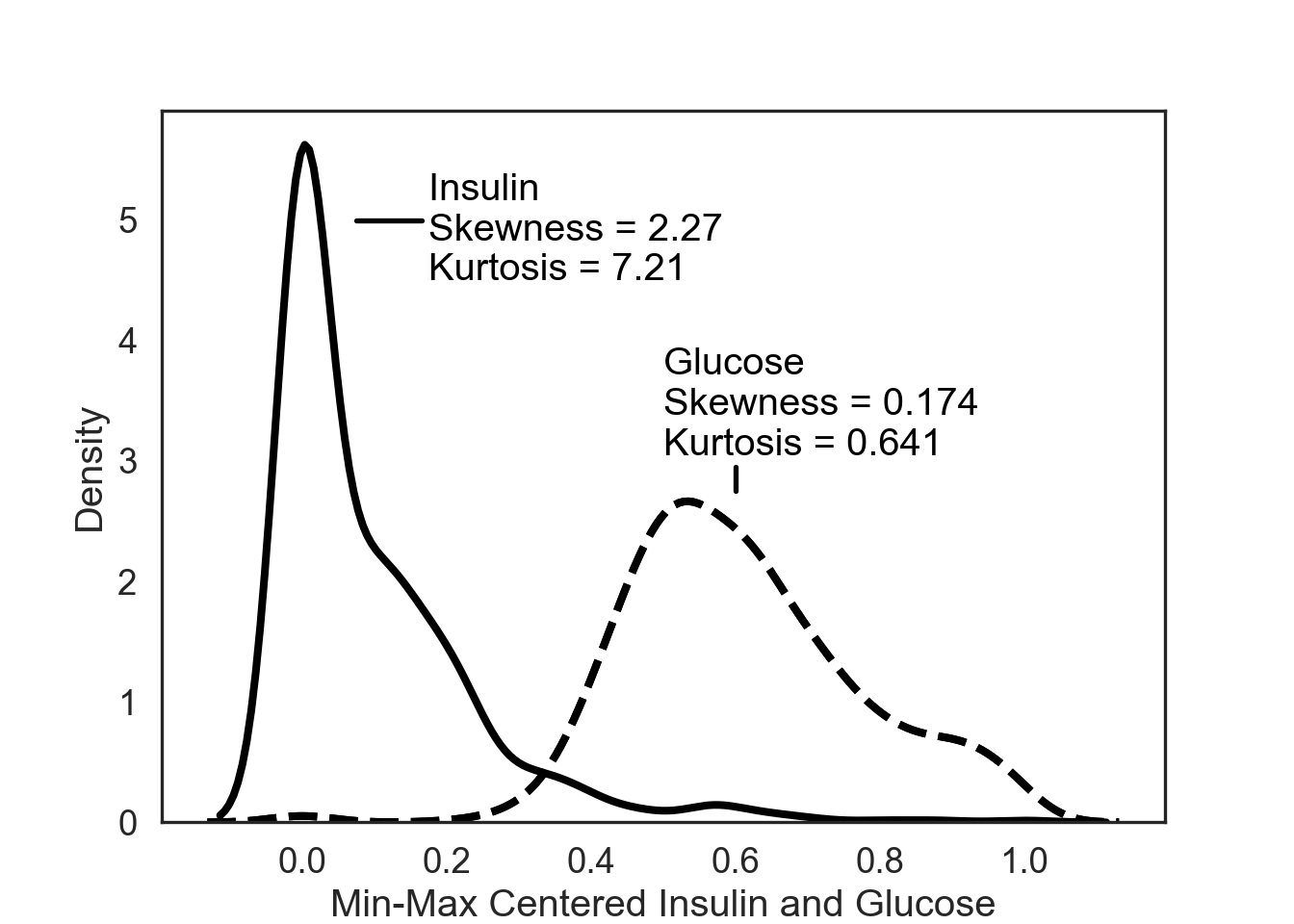
Distribution Shape

Measures of describing the shape of a distribution, usually compared to a normal distribution (bell-curve)

  • Skewness: The symmetry of the distribution

  • Kurtosis: The tailedness of the distribution

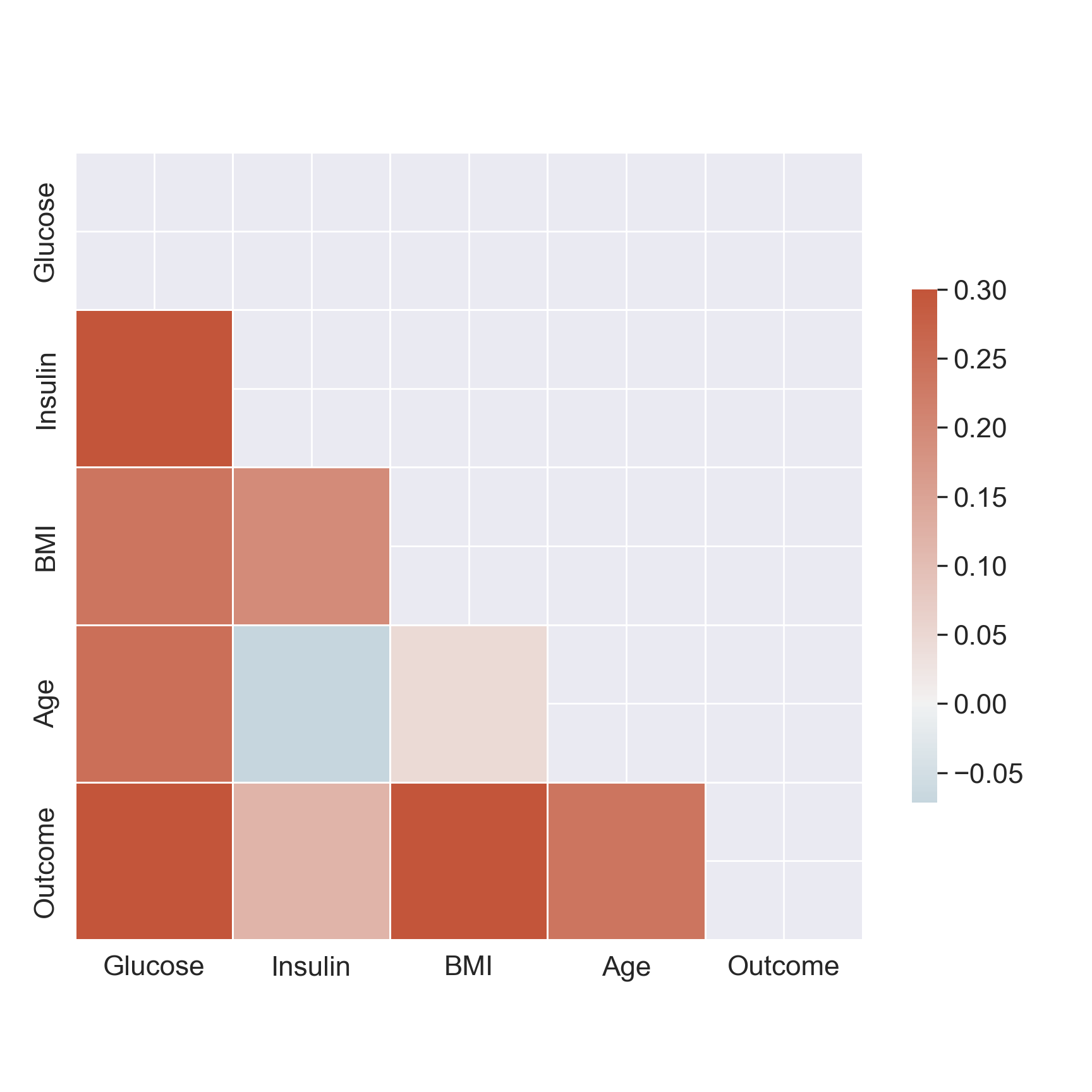
Statistical Dependence (Correlation)

Measure of causality between two random variables (statistically). Notably, we approximate causality with correlations (see correlation \(\neq\) causation)

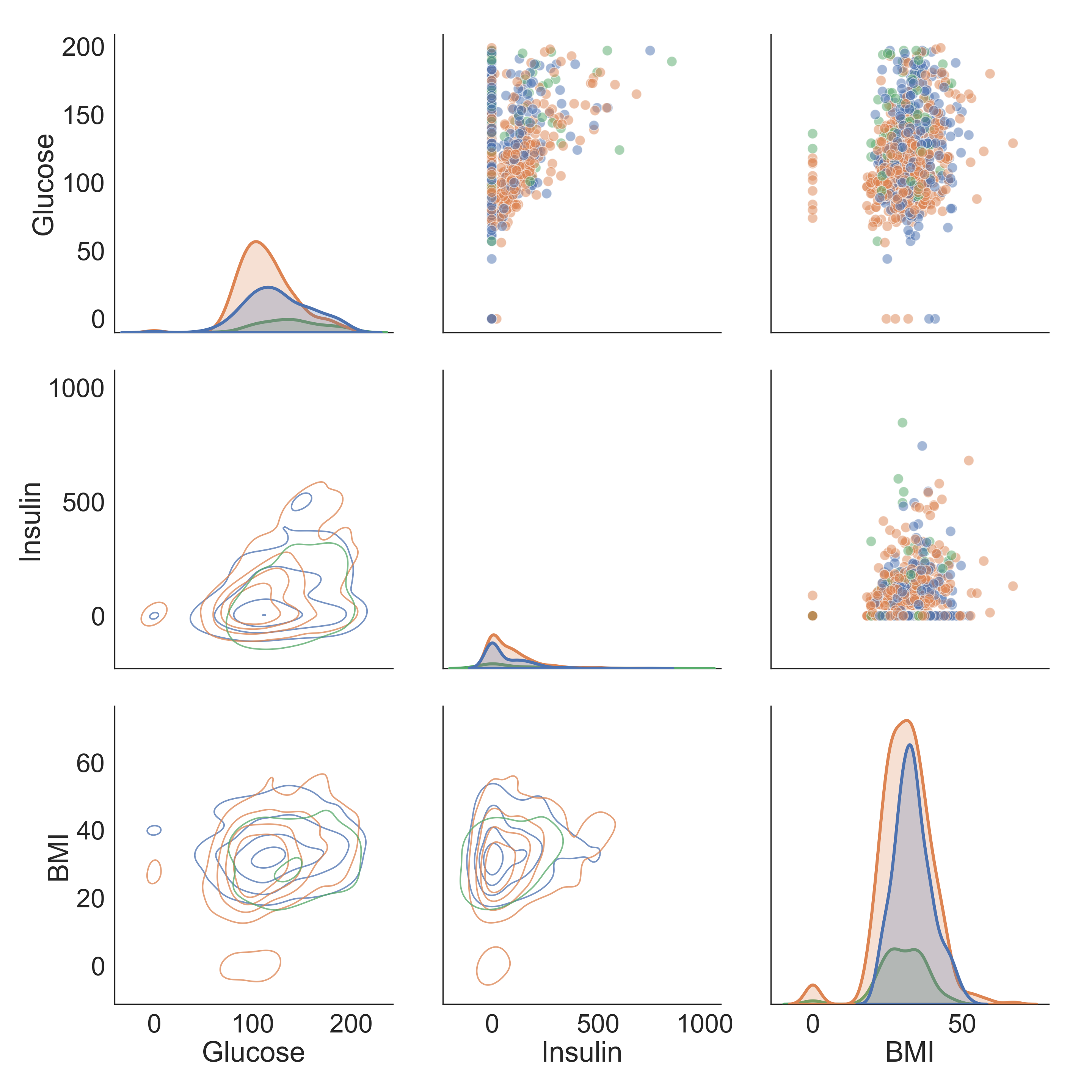
  • Numerical values, but you can compare numericals across categories (see the first plot above).

Team, The Pandas Development. 2022. Pandas-Dev/Pandas: Pandas. Zenodo. https://doi.org/10.5281/ZENODO.7093122.