DSF 2022: Statistics

Greg Chism

October 25, 2022

Statistics

Why do we need statistics?

  • Proper methods
  • Correct analysis
  • Effectively present results

Statistics

Why do we need statistics?

  • Proper methods
  • Correct analysis
  • Effectively present results?..

Road Map

  • Data and Sampling

  • Distributions

  • Central Limit Theorem

  • Statistical Significance & Power

  • Hypothesis Testing

Artwork by @allison_horst

Road Map

  • Data and Sampling

  • Distributions

  • Central Limit Theorem

  • Statistical Significance & Power

  • Hypothesis Testing

Case Study

  • Objective: Evaluate the effectiveness of cognitive-behavior therapy for chronic fatigue syndrome.

  • Participant pool: 142 patients recruited from referrals by primary care physicians and consultants to a clinic that specializes in chronic fatigue syndrome.

  • Actual participants (N): 60 of 142 patients entered the study, some were excluded for various reasons and others refused to participate

Case Study: Results

Distribution of patients with good outcomes at 6-month follow-up. 7 patients dropped out of the study: 3 from treatment, 4 from control.

  • Good outcomes in treatment: \(19/27 \approx 0.70 \to 70%\)
  • Good outcomes in control group: \(5/26 \approx 0.19 \to 19\)

Conclusion?

Are the results generalizable to all with chronic fatigue syndrome?

  • Only volunteers with specific characteristics
  • Not generalizable, but the results are encouraging
  • What next?

Data Types

Artwork by @allison_horst

Data Types

Artwork by @allison_horst

Sampling: Simple random

Sampling: Stratified

Sampling: Clustered

Sampling: Multistaged

Sampling vs. Selection

Sampling vs. Selection

Sampling vs. Selection

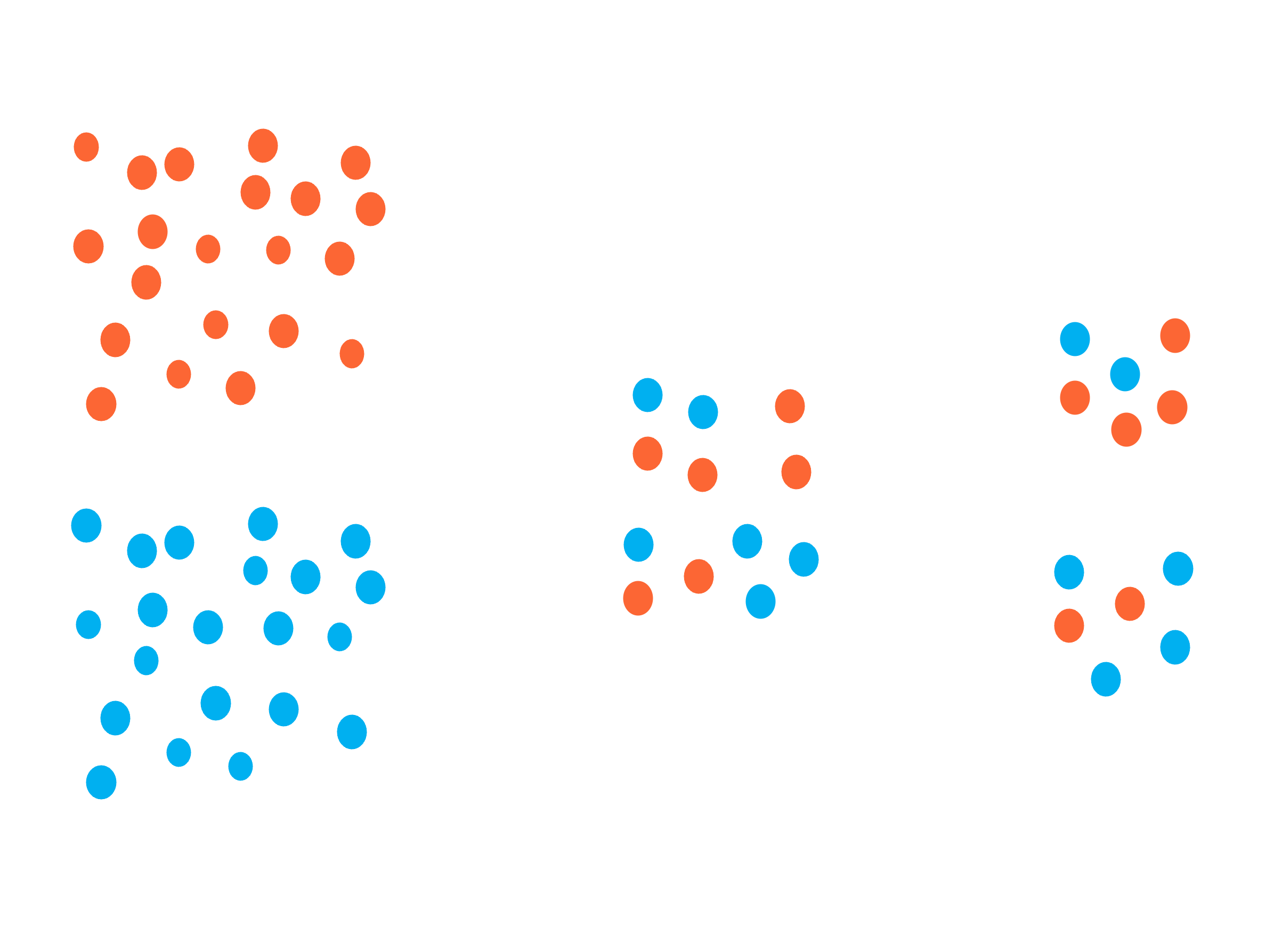
Types of Variables

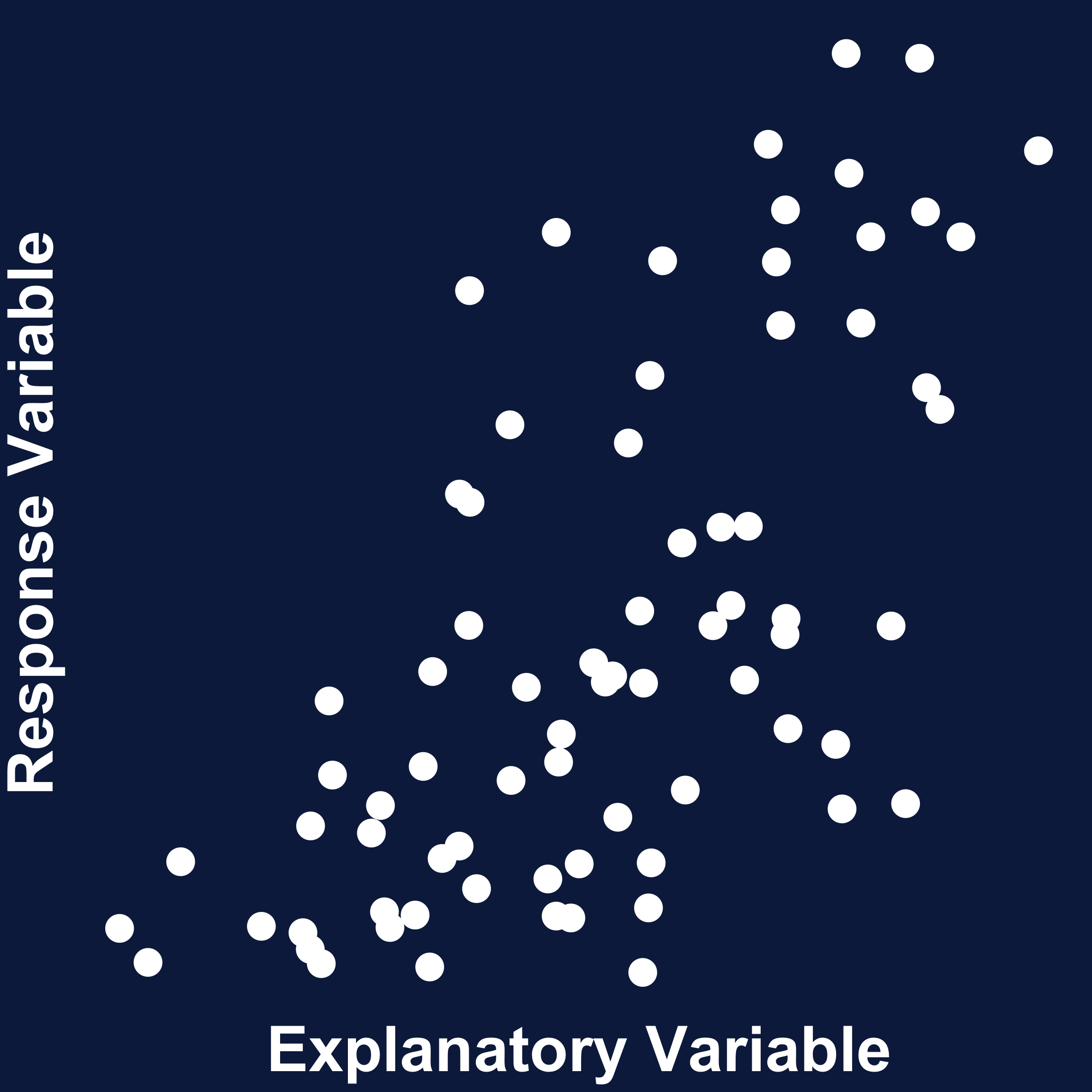
  • Response variable: variable that is predicted by another
  • Explanatory variable: variable that predicts the response variable

Road Map

  • Data and Sampling

  • Distributions

  • Central Limit Theorem

  • Statistical Significance & Power

  • Hypothesis Testing

Artwork by @allison_horst

Distributions: Gaussian

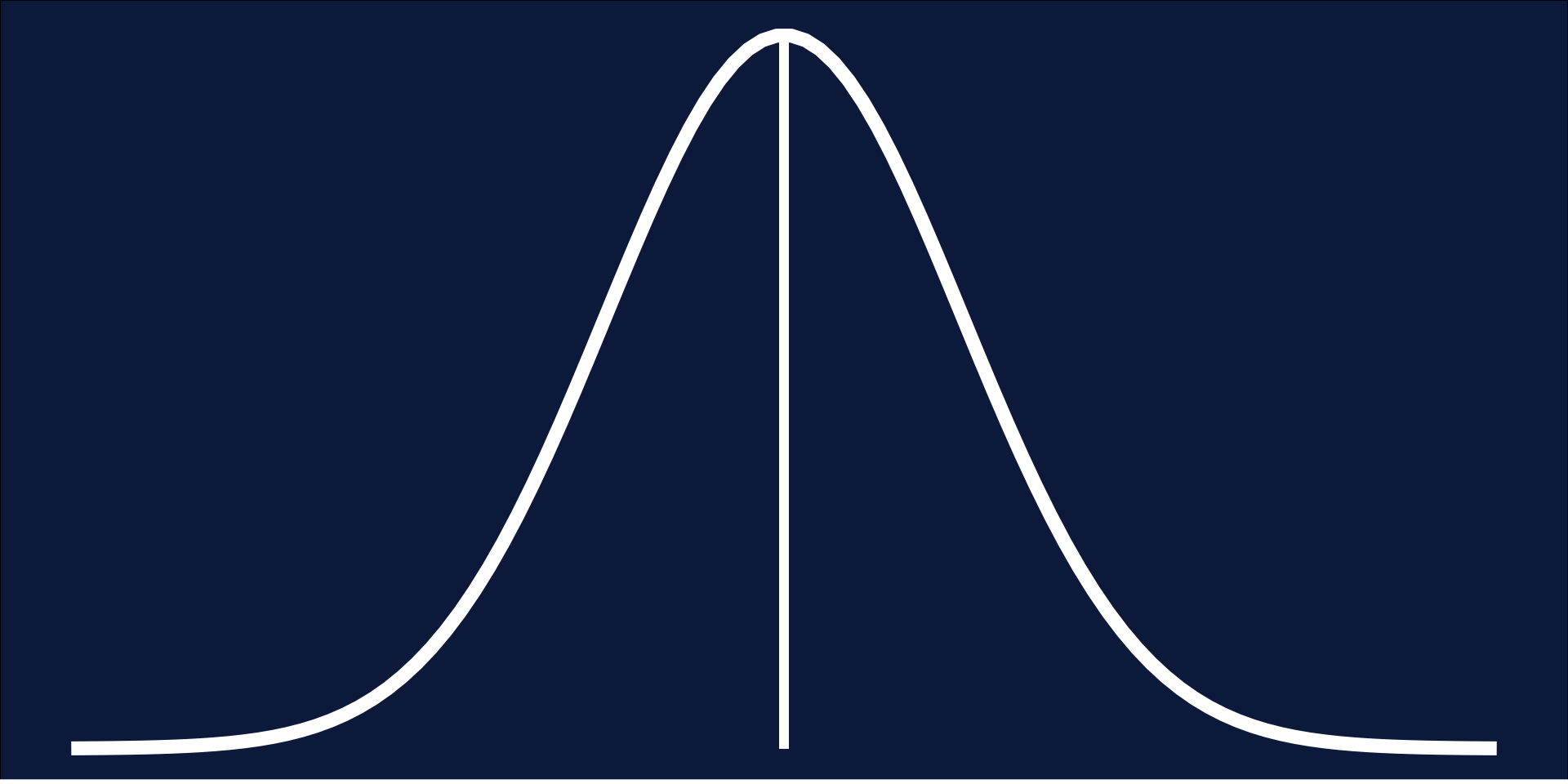
  • Symmetrical
  • Mean = Median
  • No changes to data needed

Distributions: Skewed

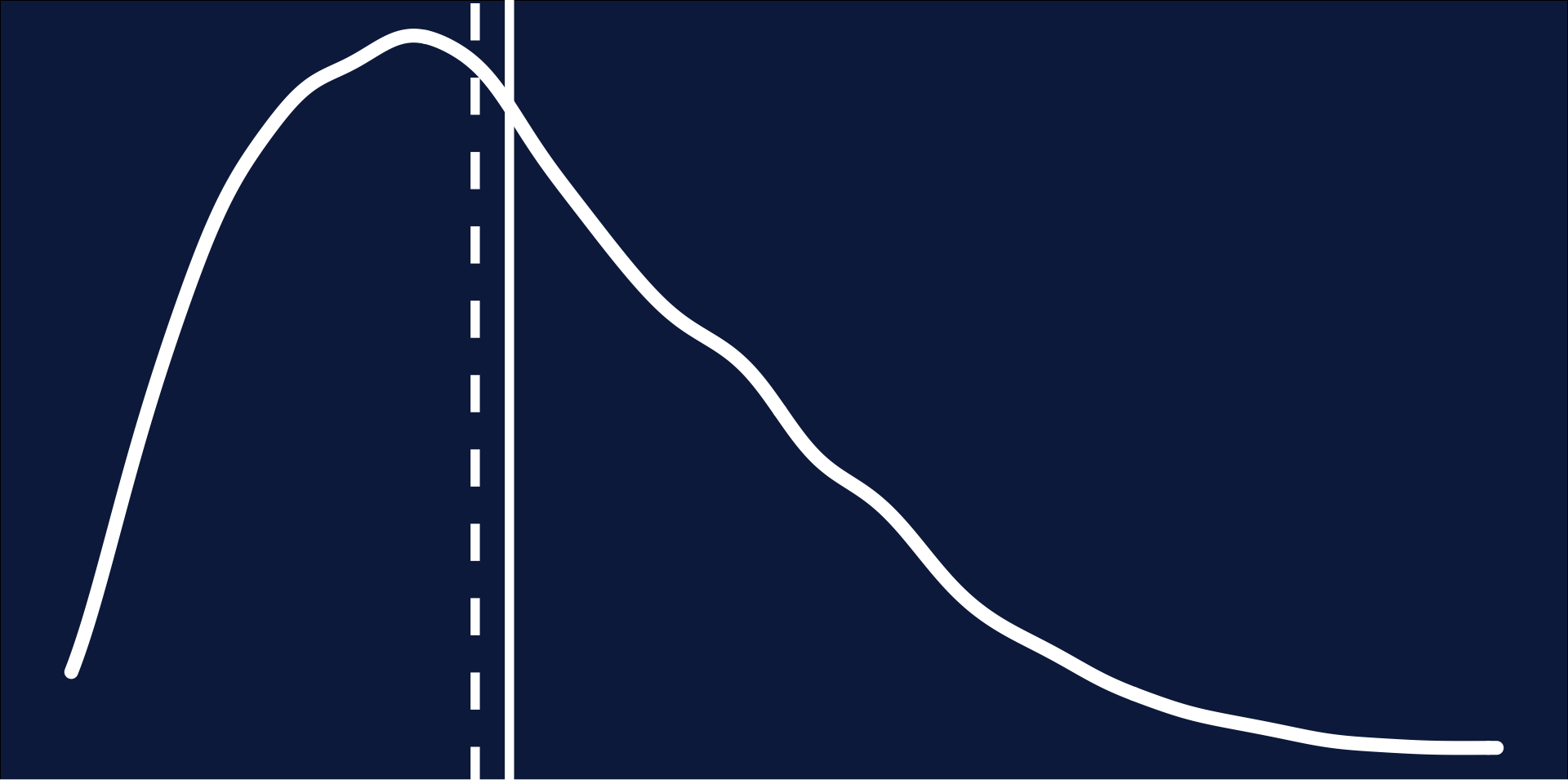
  • Not symmetrical
  • Mean = Median
  • Transform data (e.g., square-root)

Distributions: Skewed

  • Not symmetrical
  • Mean = Median
  • Transform data (e.g., square-root)

Distributions: Bimodal

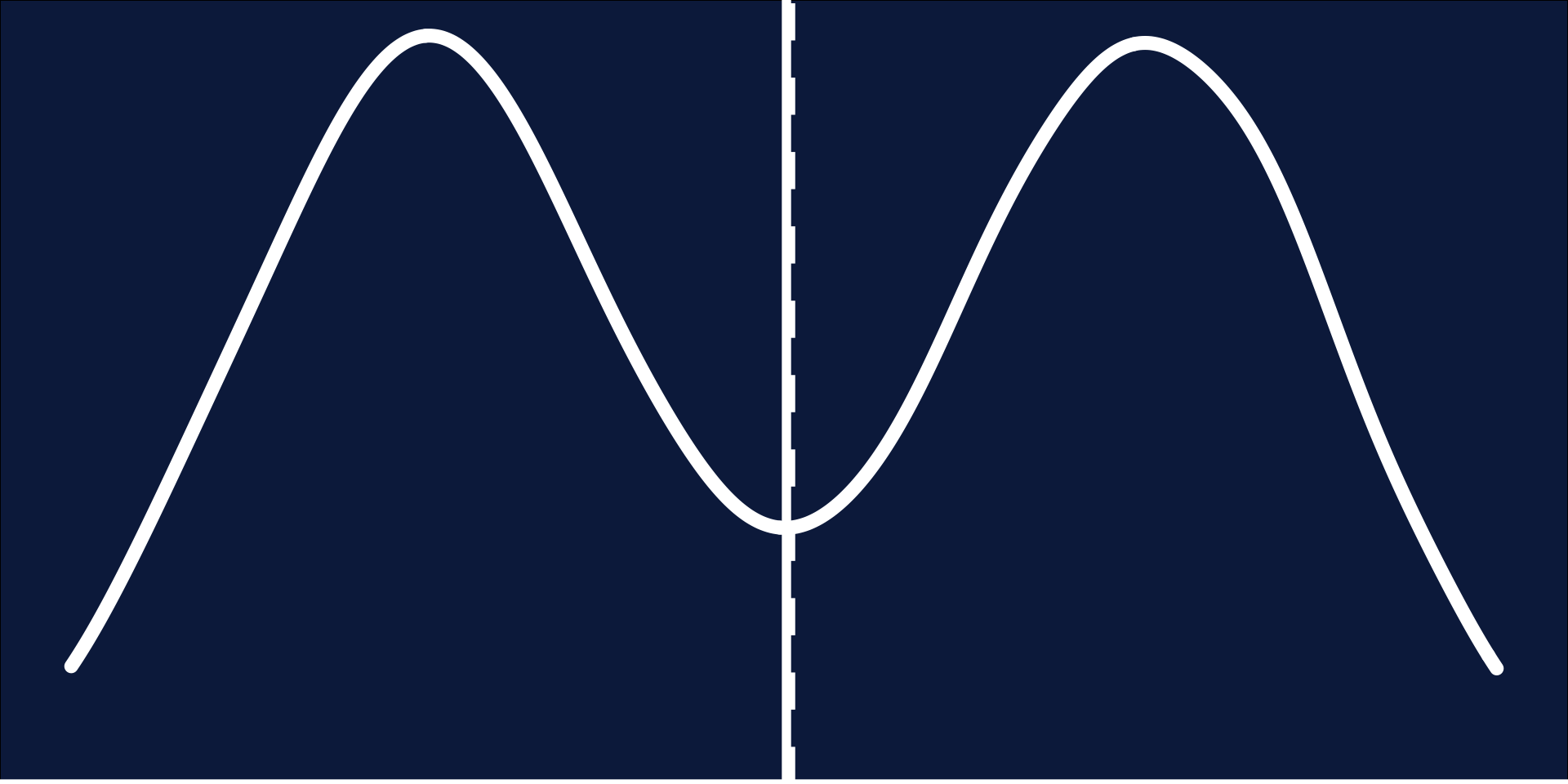
  • Symmetrical*
  • Mean = Median*
  • Break up the data

Distributions: Bimodal

  • Symmetrical*
  • Mean = Median*
  • Break up the data

Road Map

  • Data and Sampling

  • Distributions

  • Central Limit Theorem

  • Statistical Significance & Power

  • Hypothesis Testing

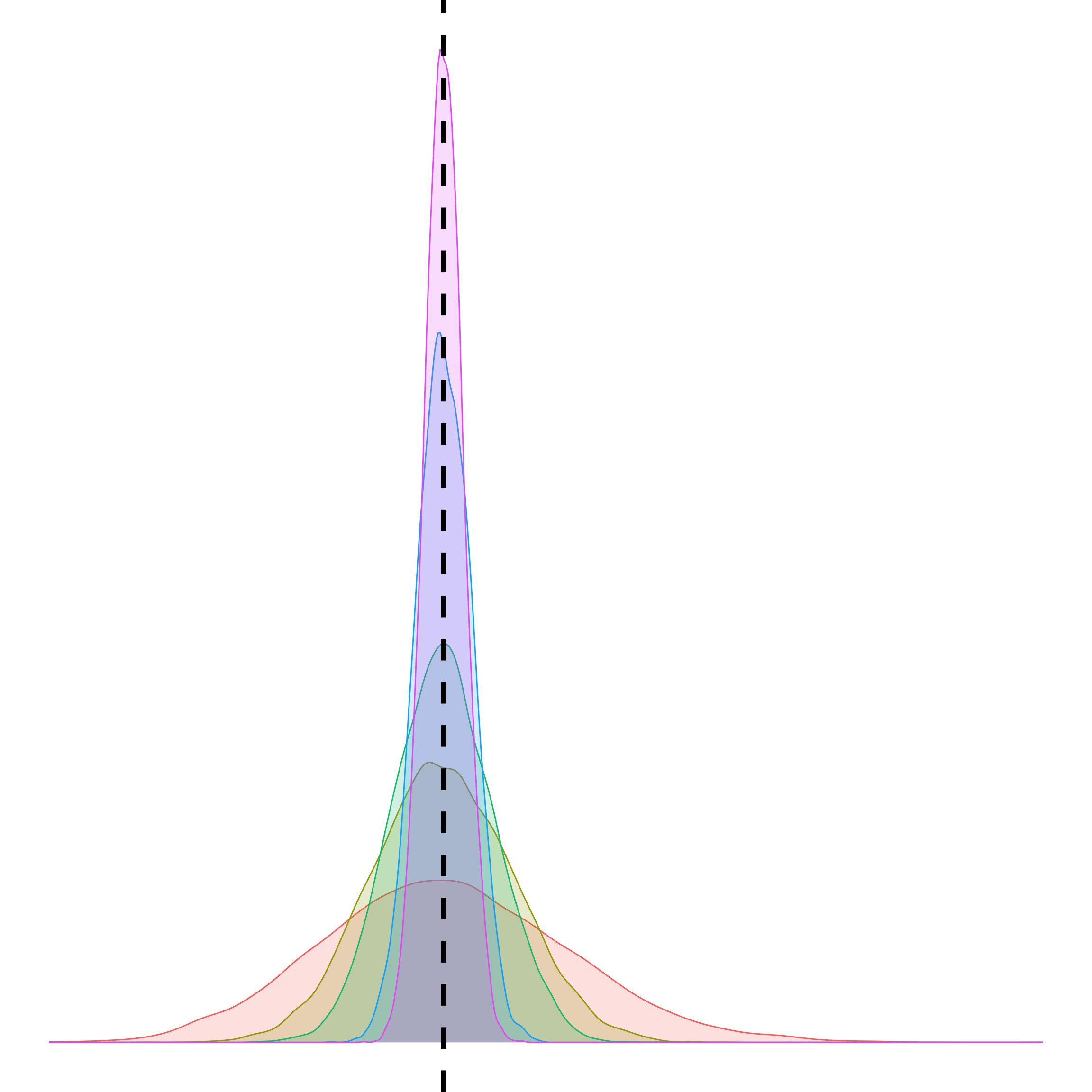
Central Limit Theorem: Uniform

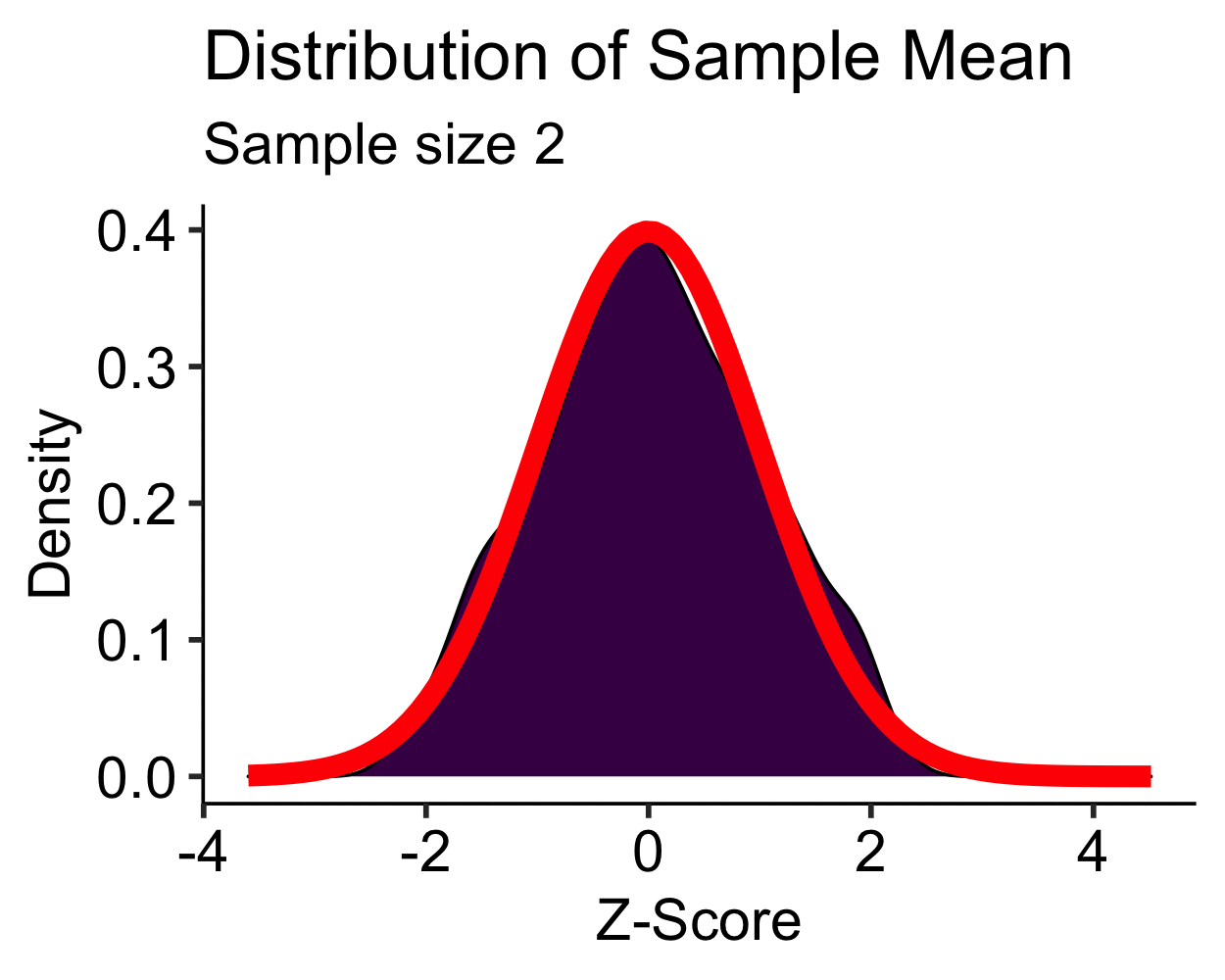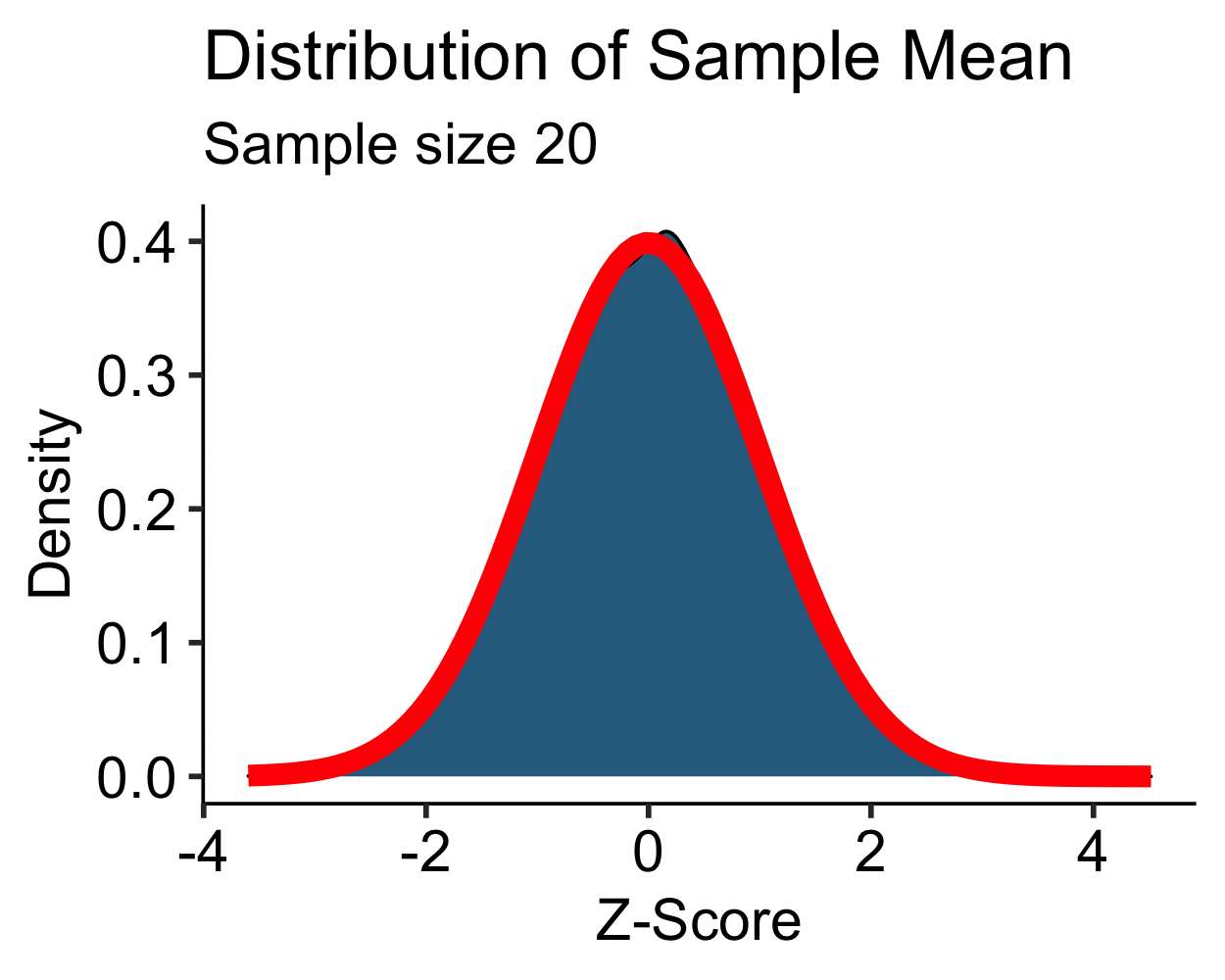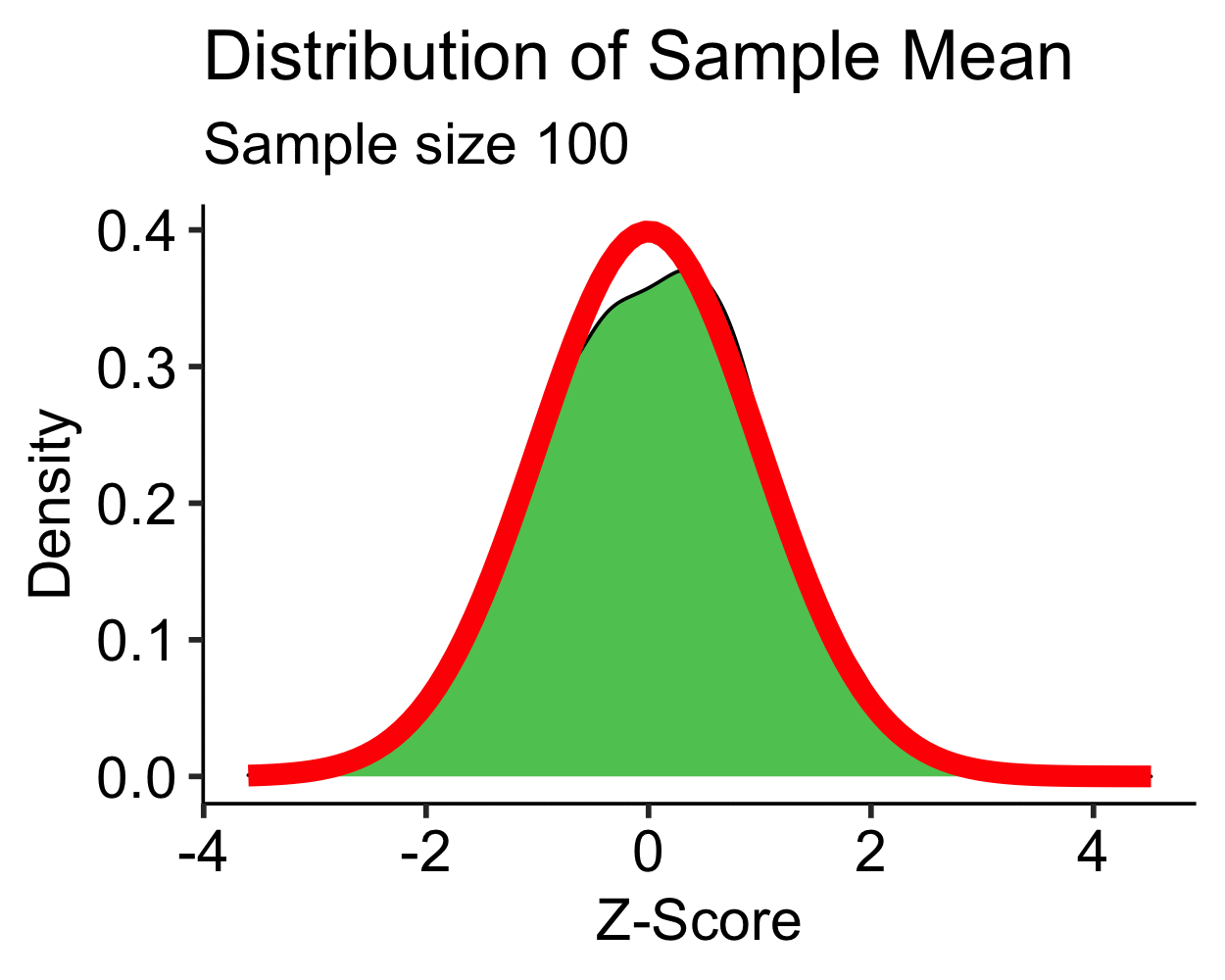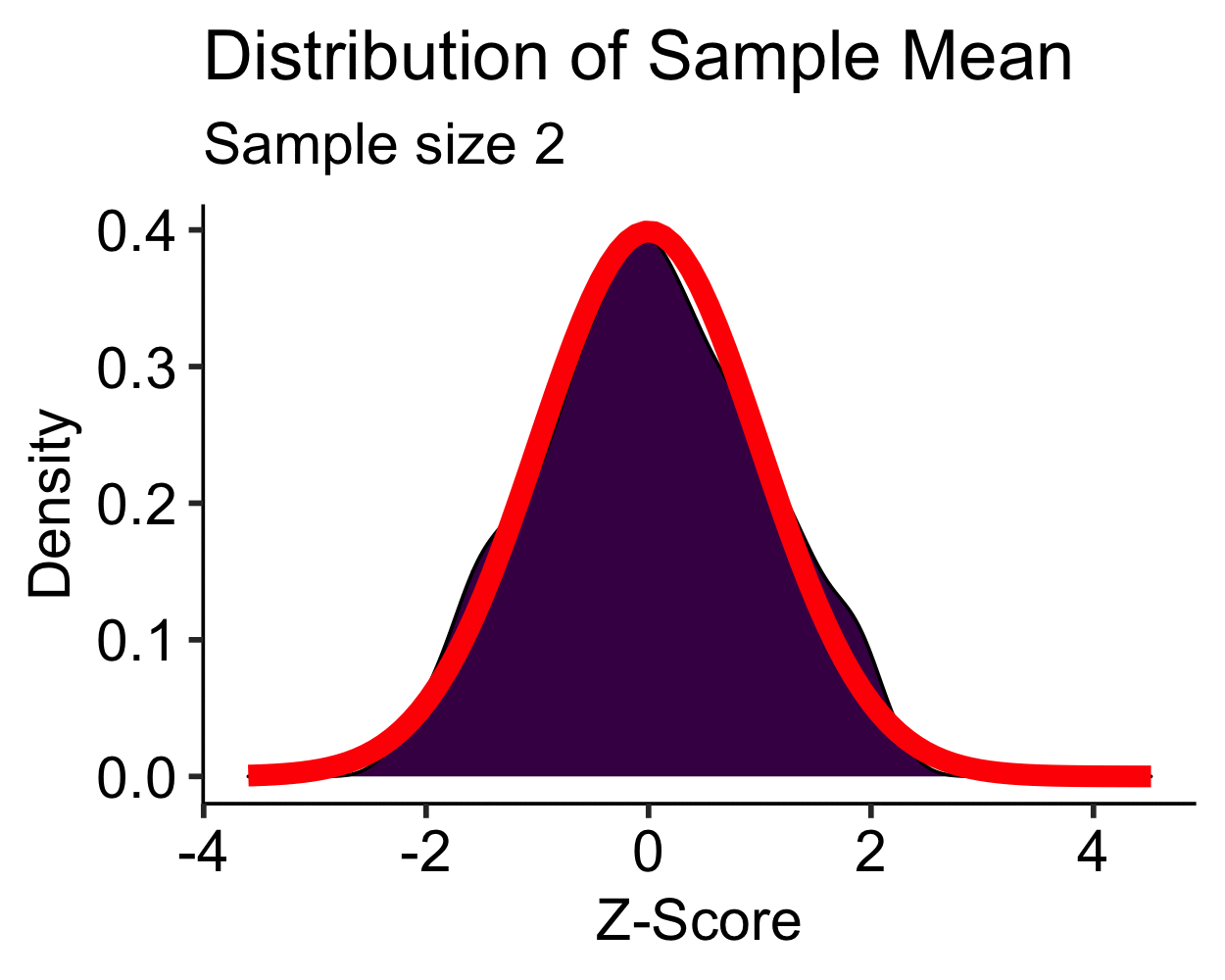
  • Uniform distribution is approximately normal with \(N > 10\)
  • \(N > 30\) is sufficient for most distributions

Central Limit Theorem: Skewed

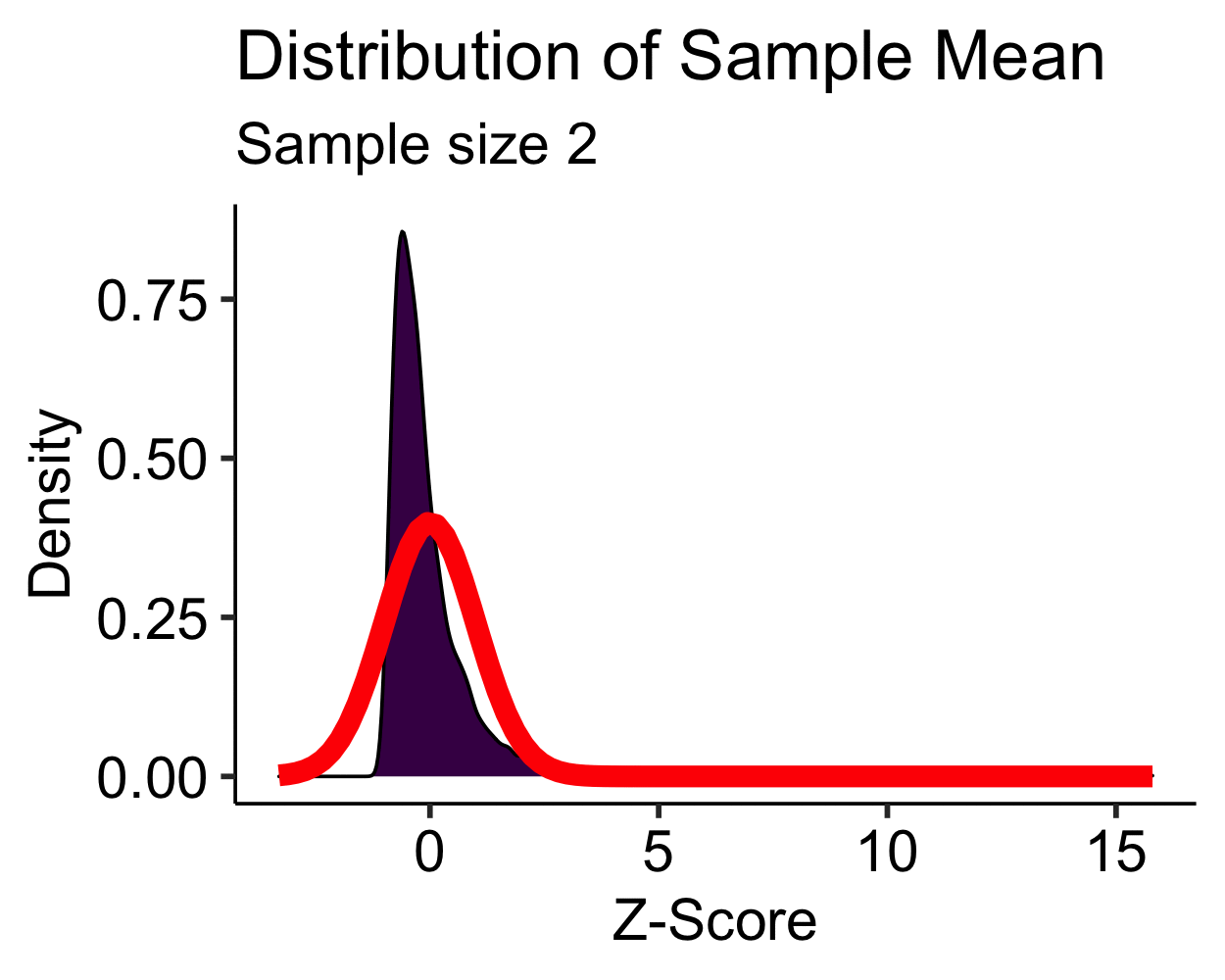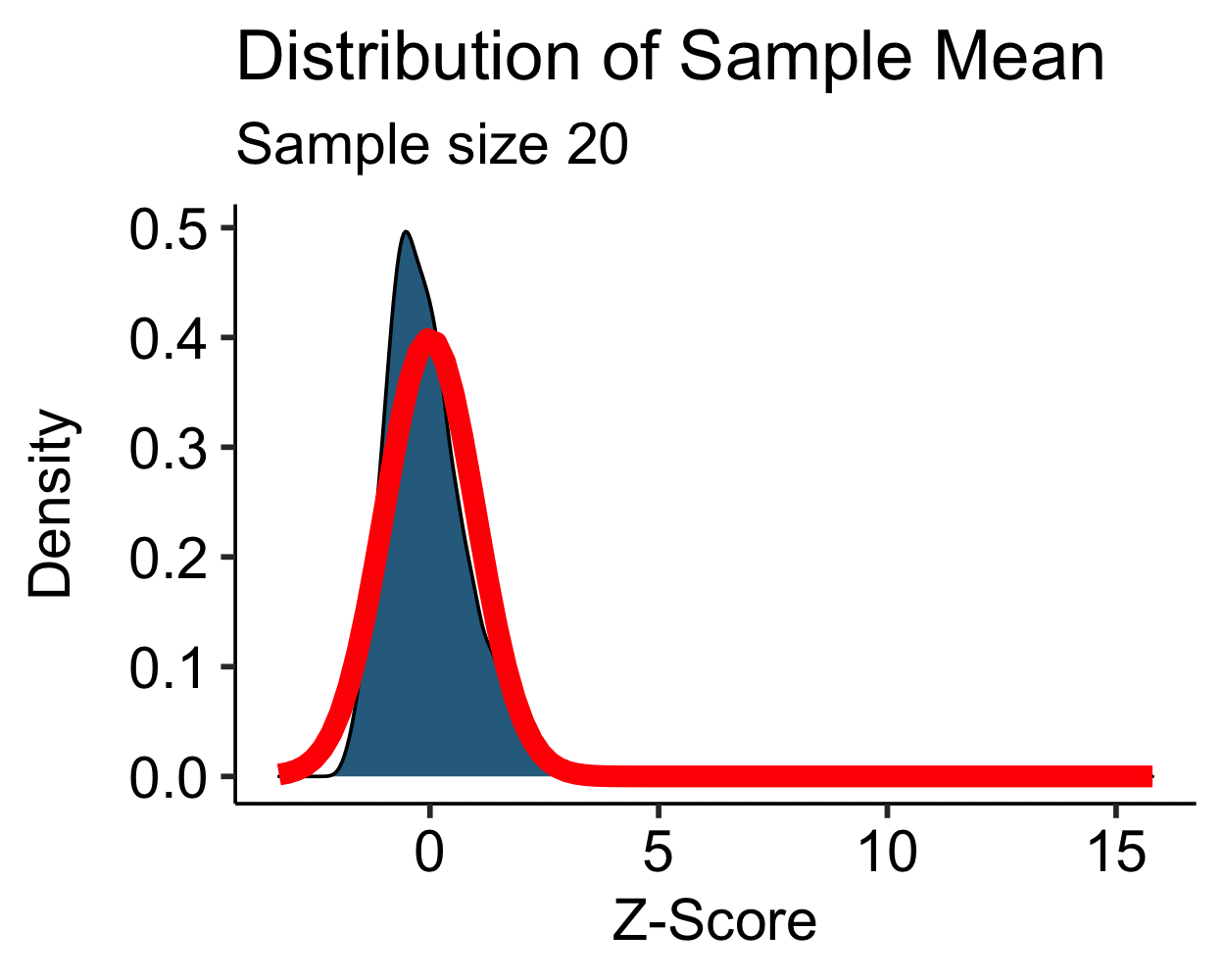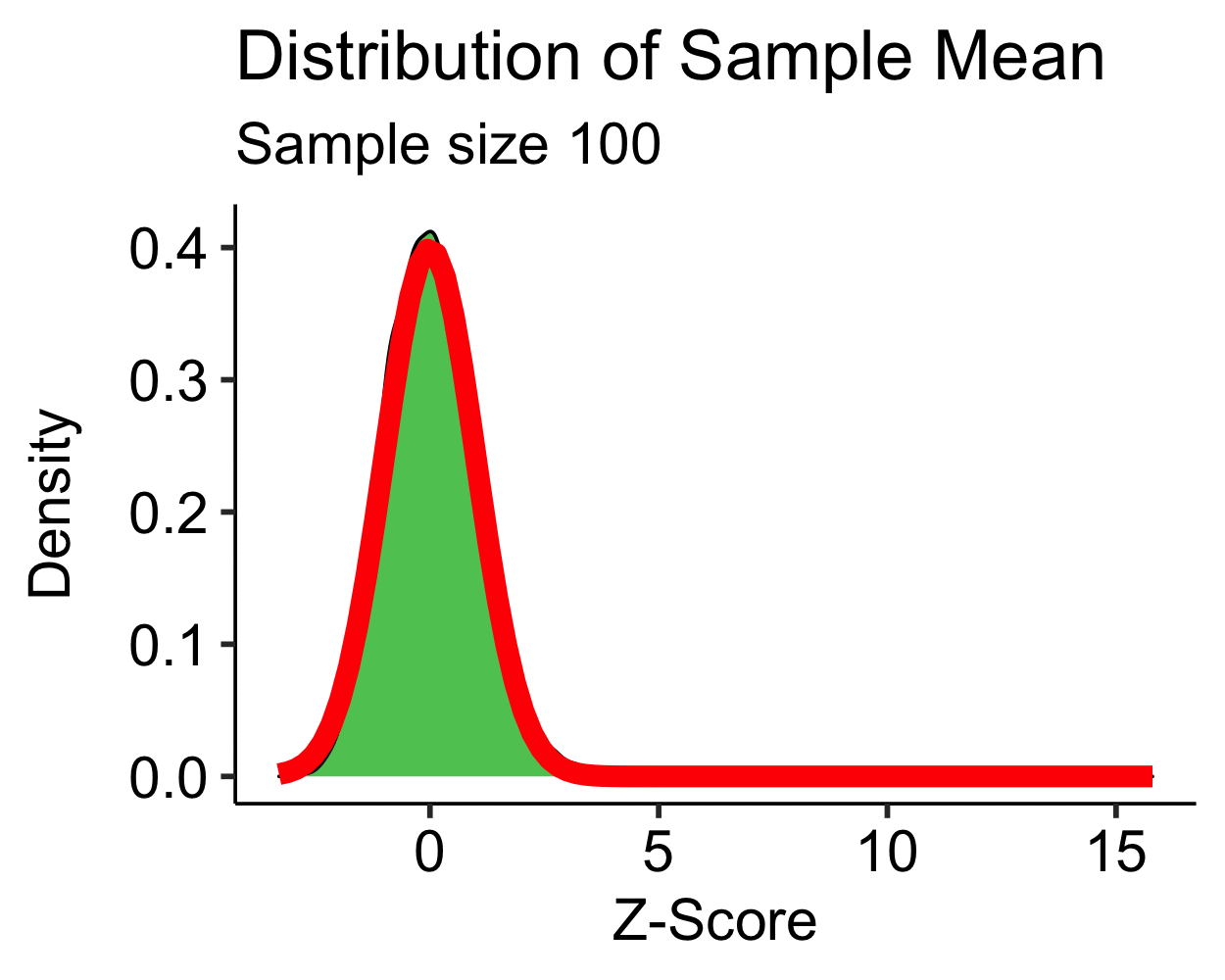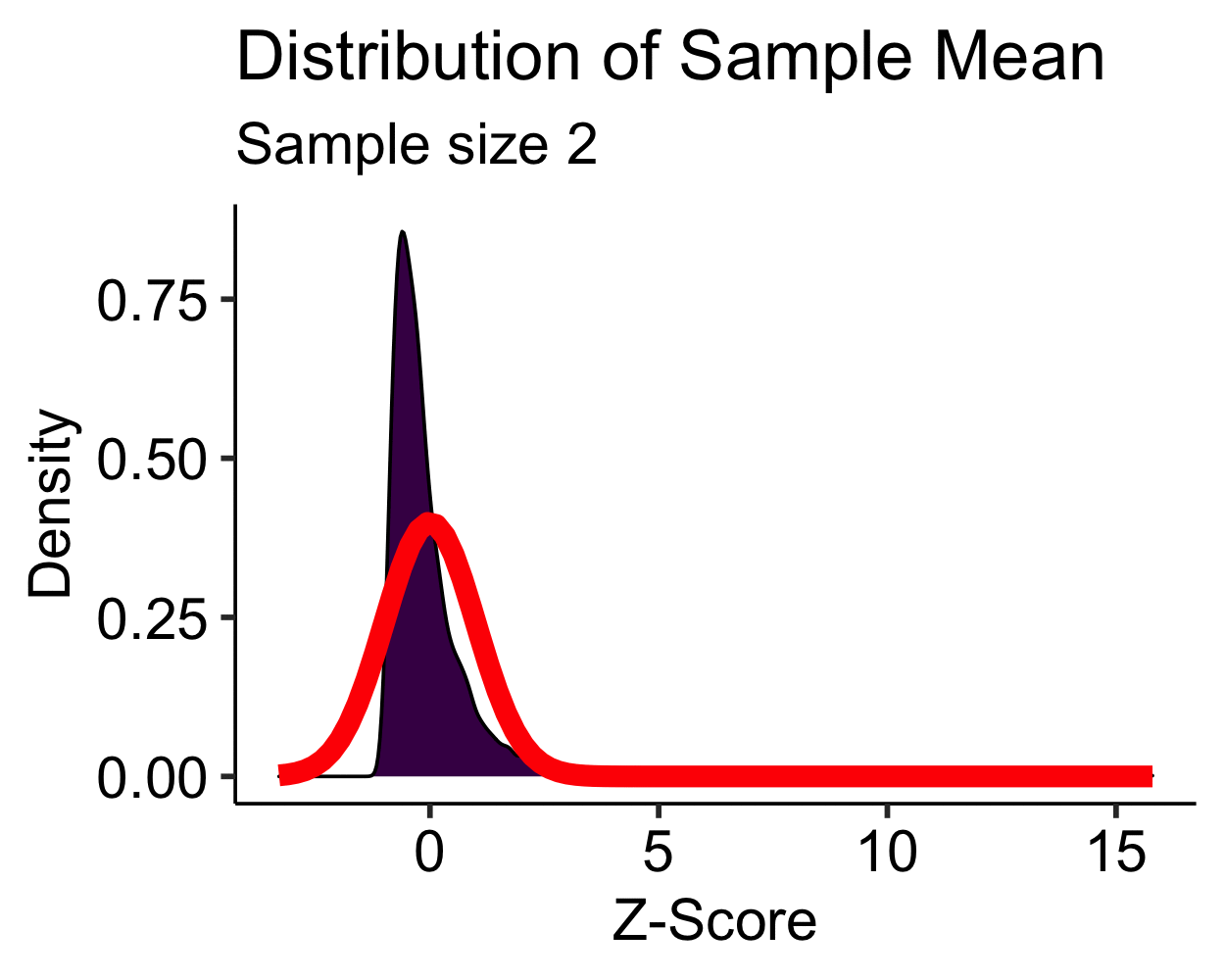
  • Skewed distribution is approximately normal with \(N > 30\)
  • Moderate to high skew may require \(N > 100\)…
  • Transformations are more feasible than increasing your sample size

Normality: 68, 95, 99.7 rule

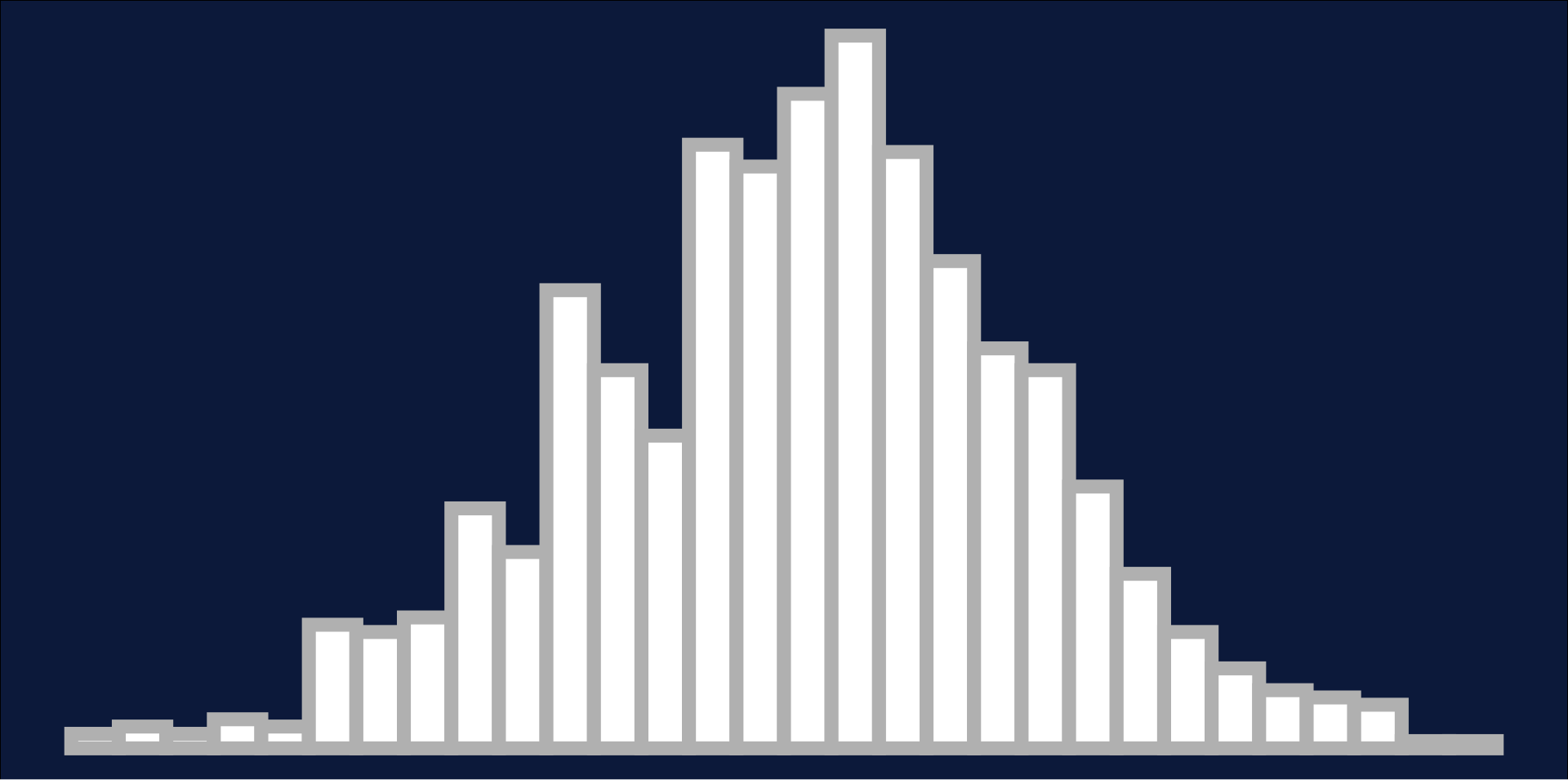
Normality: 68, 95, 99.7 rule

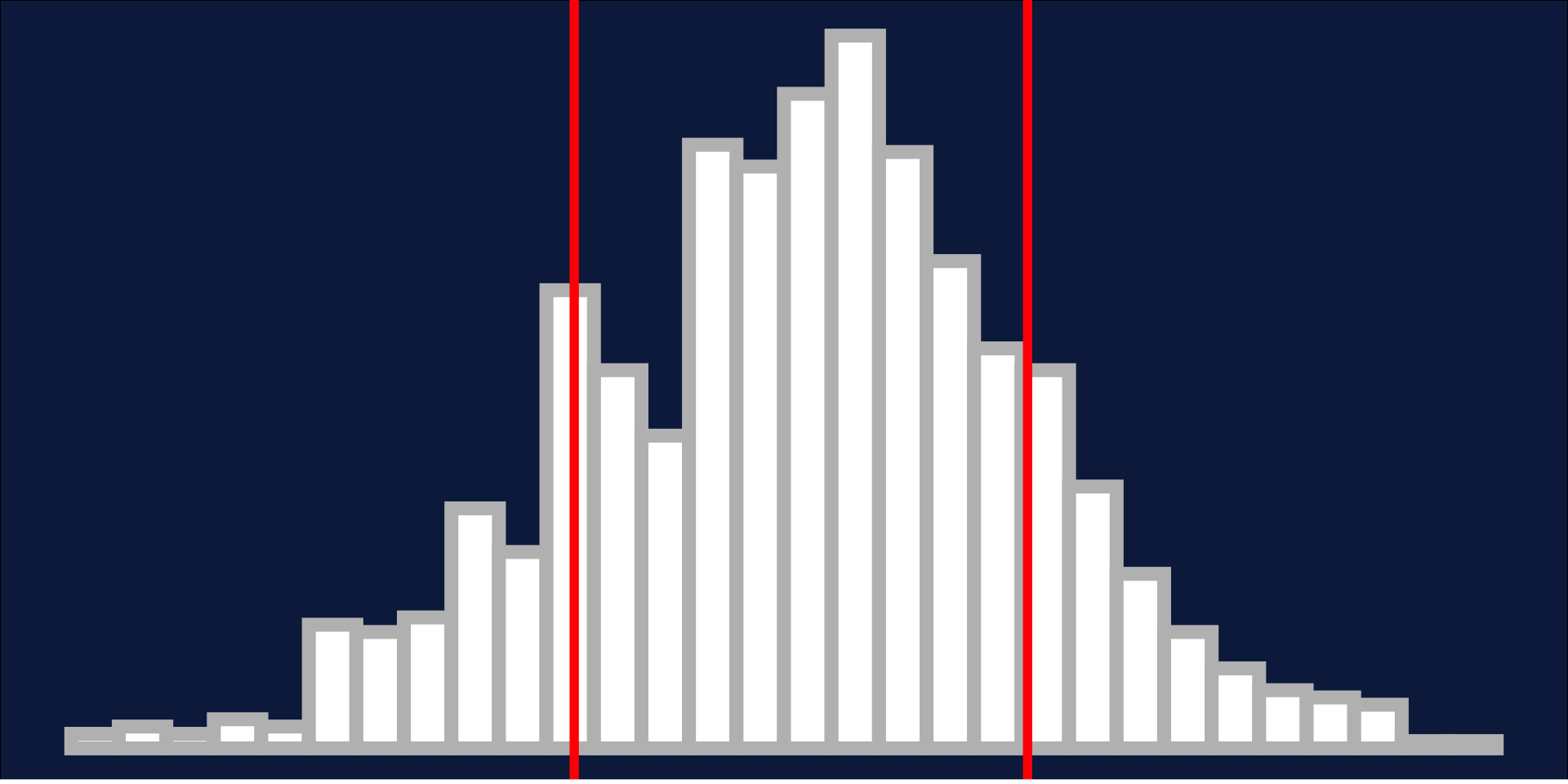
  • 1 Standard deviation = 68%

Normality: 68, 95, 99.7 rule

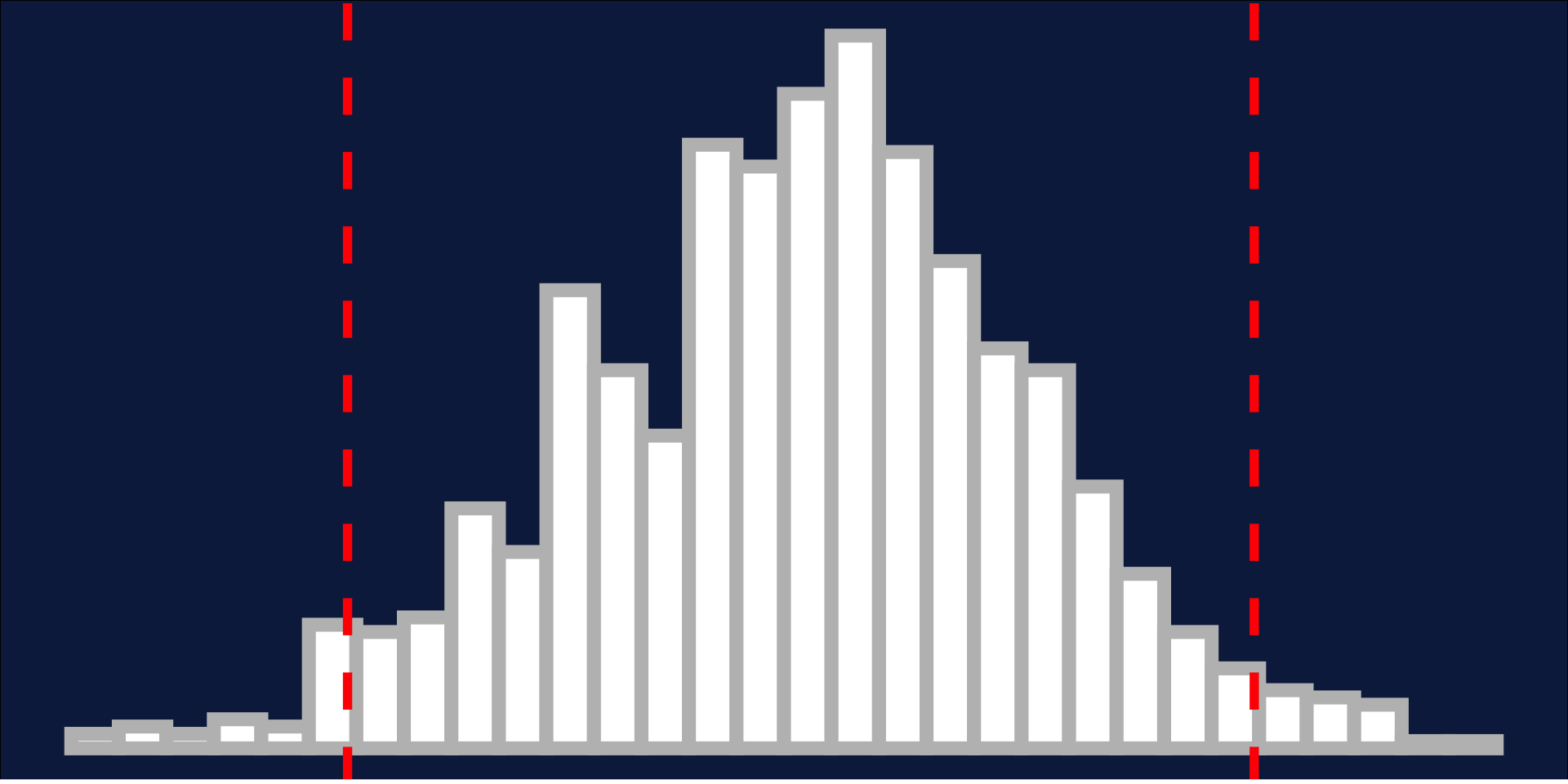
  • 1 Standard deviation = 68%
  • 2 Standard deviations = 95%

Normality: 68, 95, 99.7 rule

  • 1 Standard deviation = 68%
  • 2 Standard deviations = 95%
  • 3 Standard deviations = 99.7%

Normality: 68, 95, 99.7 rule

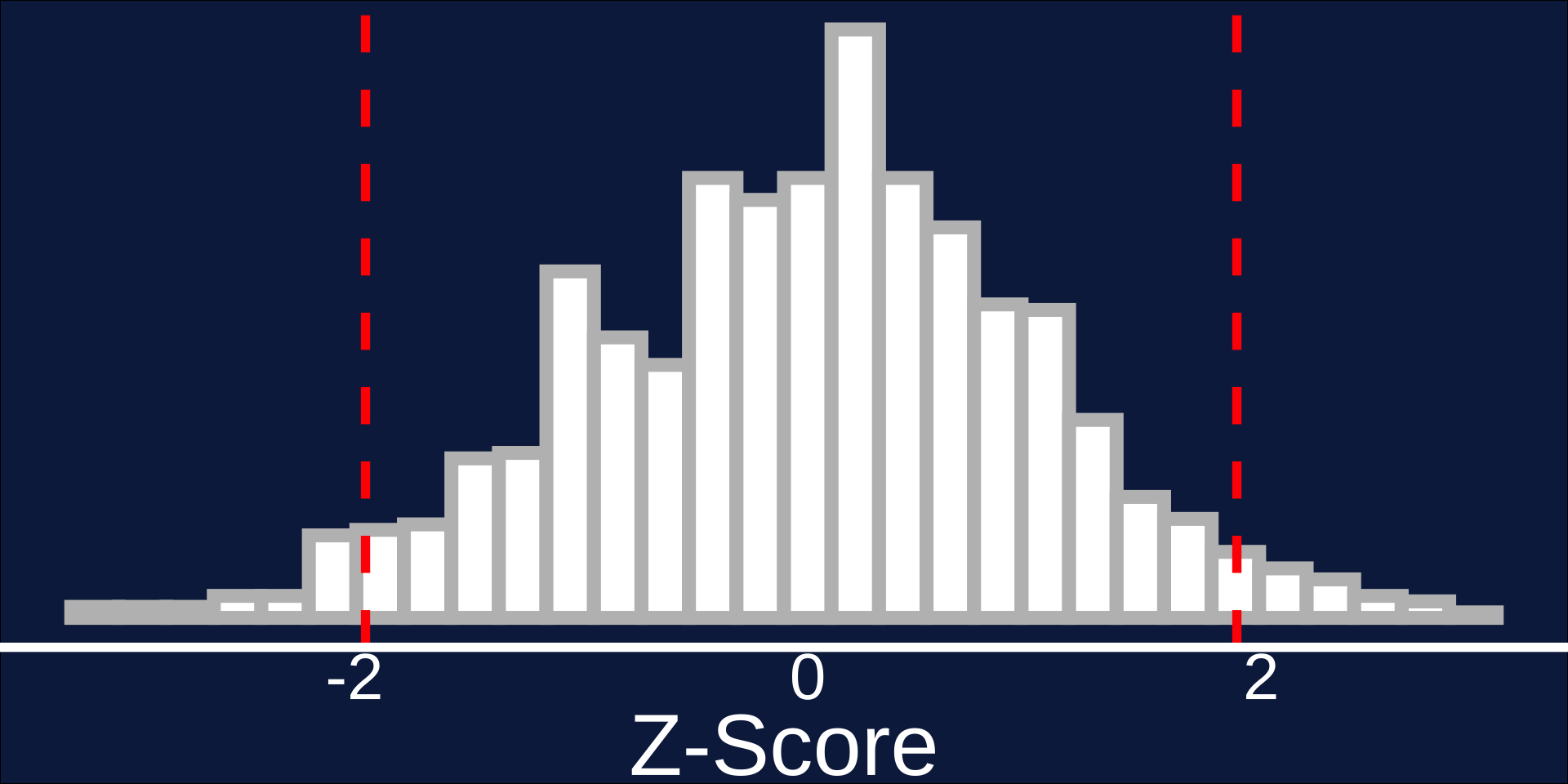
Z-Score

The number of standard deviations a value falls above or below the mean - e.g., 2 standard deviations: \(Z = 2\)

Road Map

  • Data and Sampling

  • Distributions

  • Central Limit Theorem

  • Statistical Significance & Power

  • Hypothesis Testing

Artwork by @allison_horst

P-Values

What is the likelihood that your data is different that expected from random variation?

P-Values

What is the likelihood that your data is different that expected from random variation?

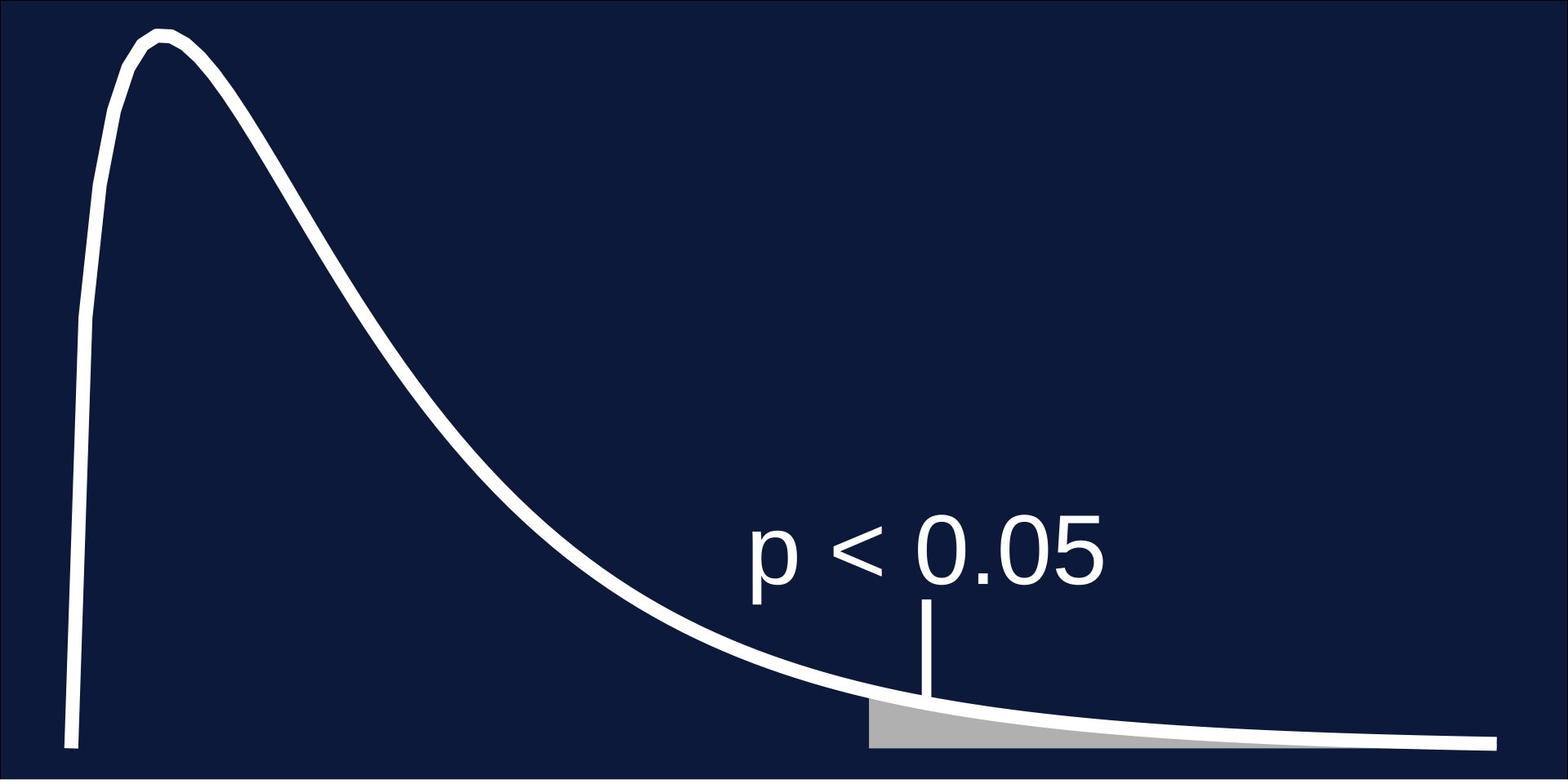
F-Distribution

  • Probability of observing data at least as favorable to the alternative hypothesis, if the null hypothesis is not true.

  • Translation: The relationship that we find is not from random chance.

Confidence Intervals

  • Significance as \(< 0.05\) we are saying that 5% of our conclusions will be incorrect.
  • This means that we can have 95% Confidence that our samples will contain the true value of a statistic from the population.
  • Example: we collect 30 samples and measure the mean \(\bar{X}\), so 27.5 of those samples will contain the population mean \(\mu\)

Confidence Intervals

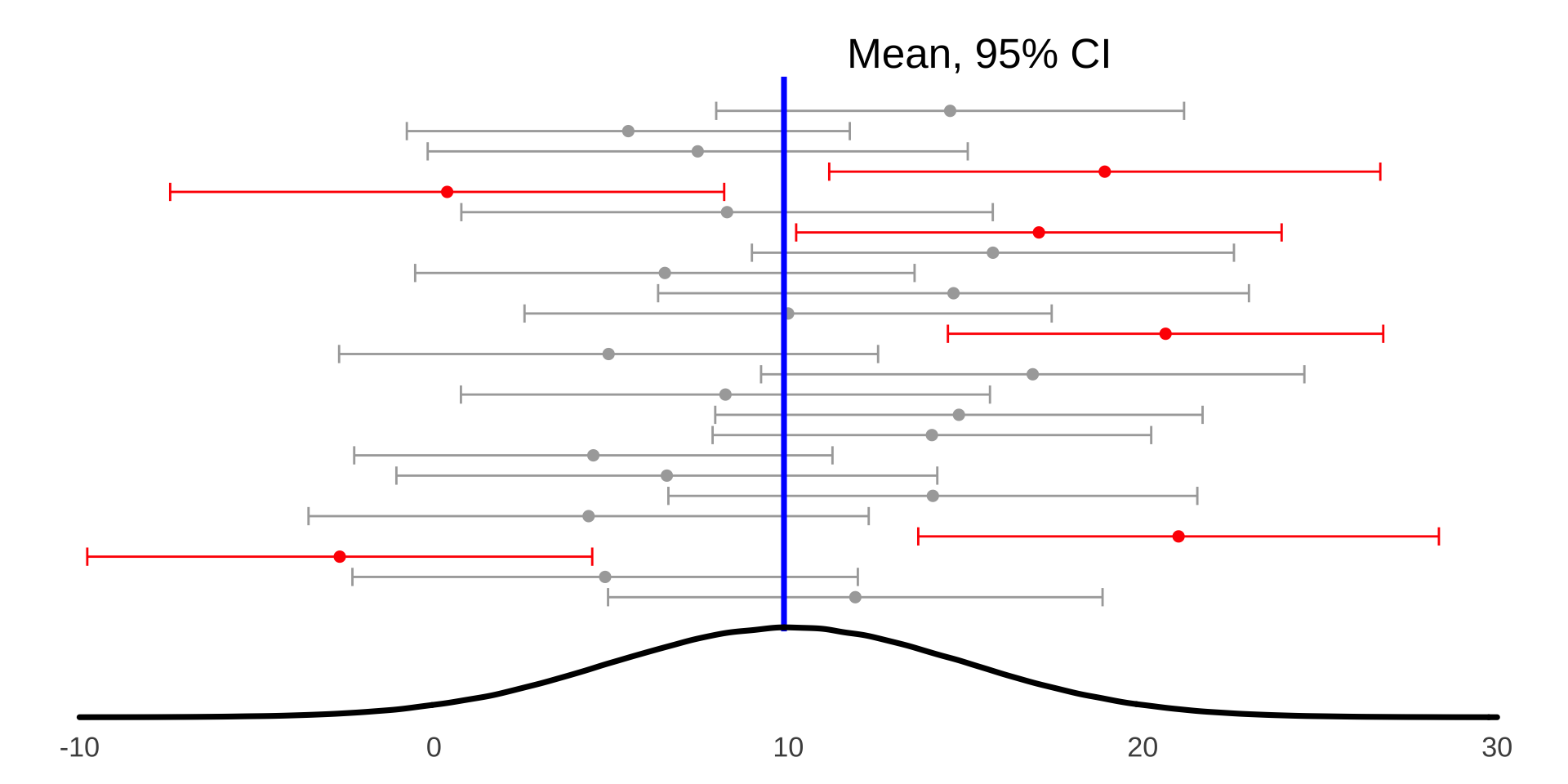
Statistical Error

Statistical Error

Statistical Error

Statistical Error

  • A Type I Error is rejecting the null hypothesis when \(H_0\) is true.

Statistical Error

  • A Type I Error is rejecting the null hypothesis when \(H_0\) is true

  • A Type II Error is rejecting the null hypothesis when \(H_A\) is true

Statistical Error: Type I Error

Artwork by @allison_horst

Statistical Error: Type II Error

Artwork by @allison_horst

Statistical Power

Power = 1 - Type II Error

  • Low Statistical Power: Large risk of committing Type II errors, e.g. a false negative.
  • High Statistical Power: Small risk of committing Type II errors.

Power Analysis

https://rpsychologist.com/d3/nhst/

Statistical Power: The probability of accepting the alternative hypothesis if it is true.

Power Analysis

https://rpsychologist.com/d3/nhst/

  • Effect Size: The strength of a result present in the population.

Power Analysis

https://rpsychologist.com/d3/nhst/

  • Effect Size: The strength of a result present in the population.
  • Sample Size: The number of observations in the sample.

Power Analysis

https://rpsychologist.com/d3/nhst/

  • Effect Size: The strength of a result present in the population.
  • Sample Size: The number of observations in the sample.
  • Significance: The significance level used in the

Road Map

  • Data and Sampling

  • Distributions

  • Central Limit Theorem

  • Statistical Significance & Power

  • Hypothesis Testing

Artwork by @allison_horst

Hypothesis Testing in Statistics

  • What hypothesis does statistics test?
  • How does this fit into the Scientific Method?

One-Sided Hypothesis Test

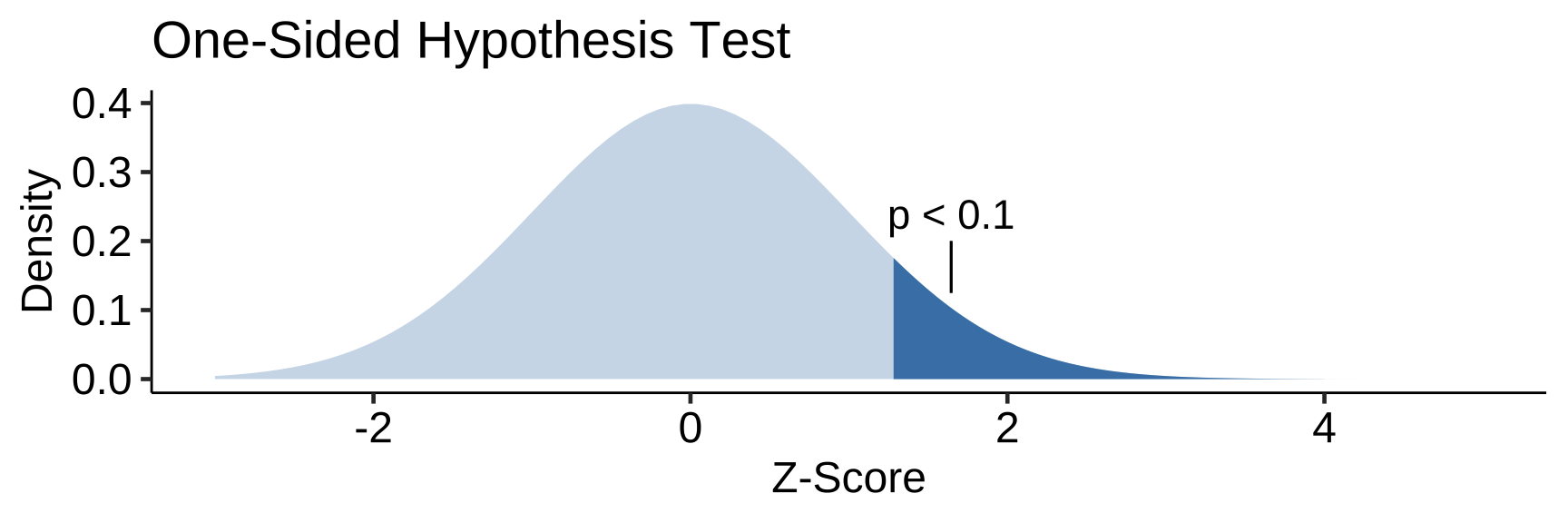
  • One-Sided/One-Tailed: p differs from one direction (and not the other)

Two-Sided Hypothesis Test

  • Two-Sided/Two-Tailed: p differs from either the left or right

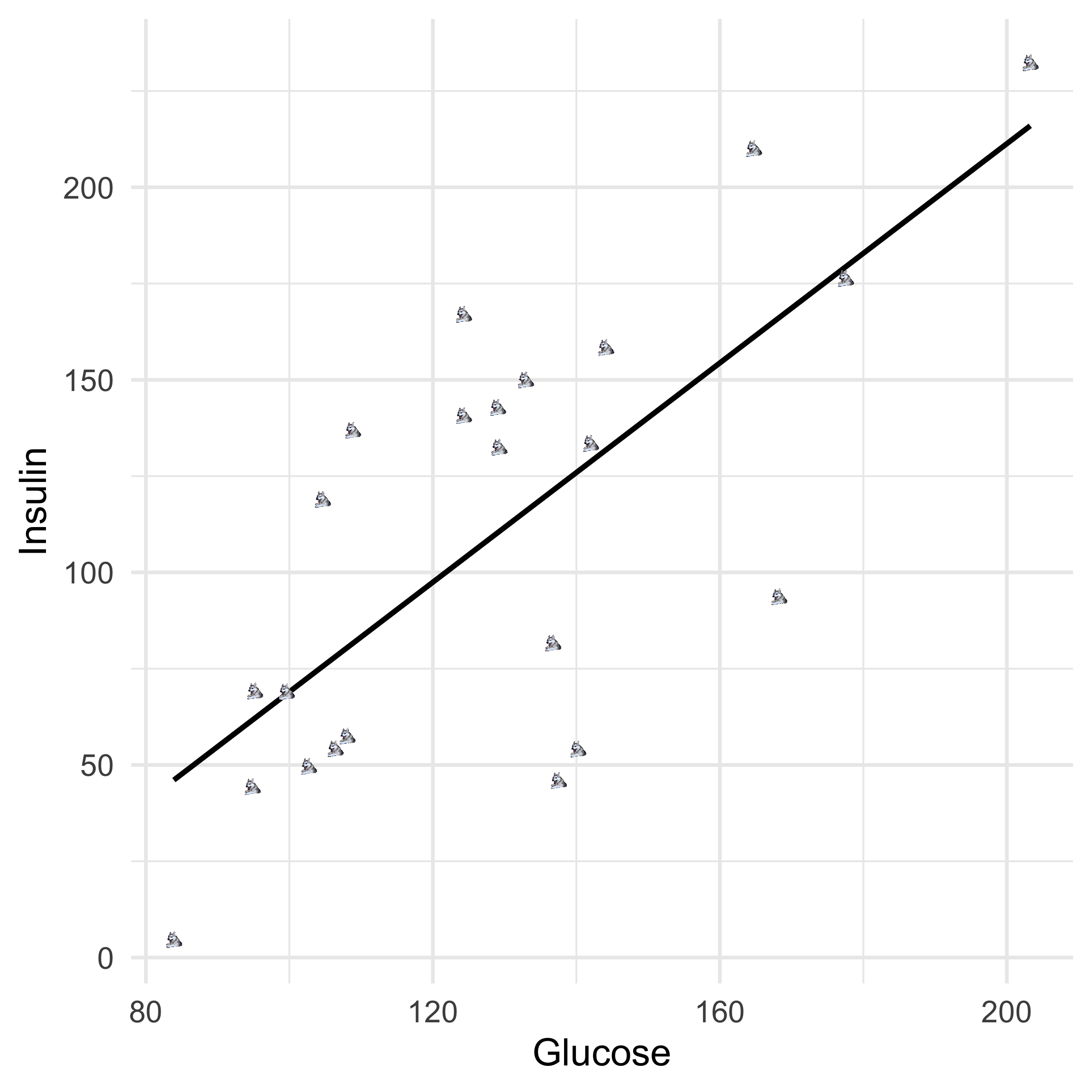
Linear Regression

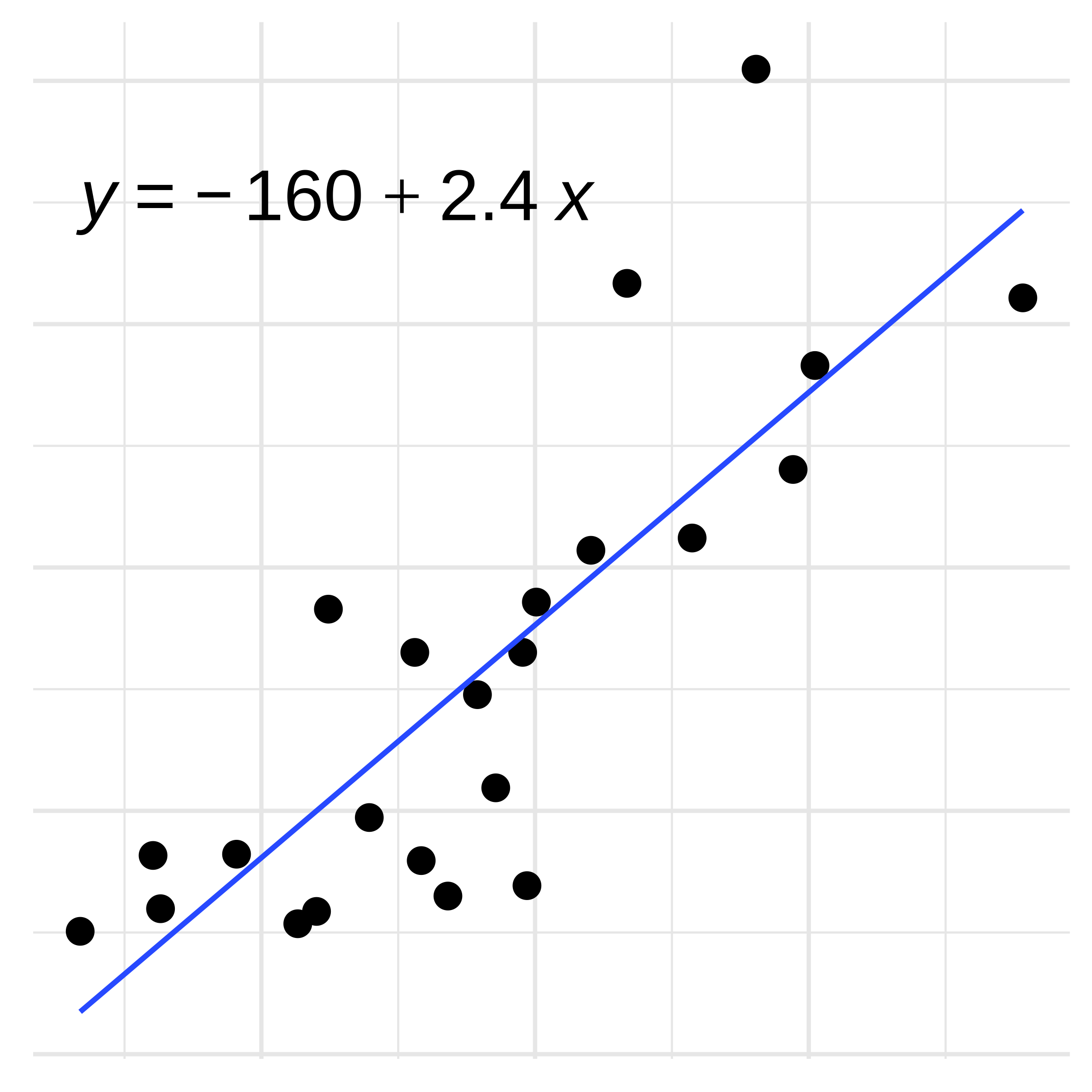
  • Relationship between numerical variables
  • \(y = \beta x + y_i\)
  • \(\beta\) is the slope
  • \(y_i\) is the y-intercept

Linear Regression: Residuals

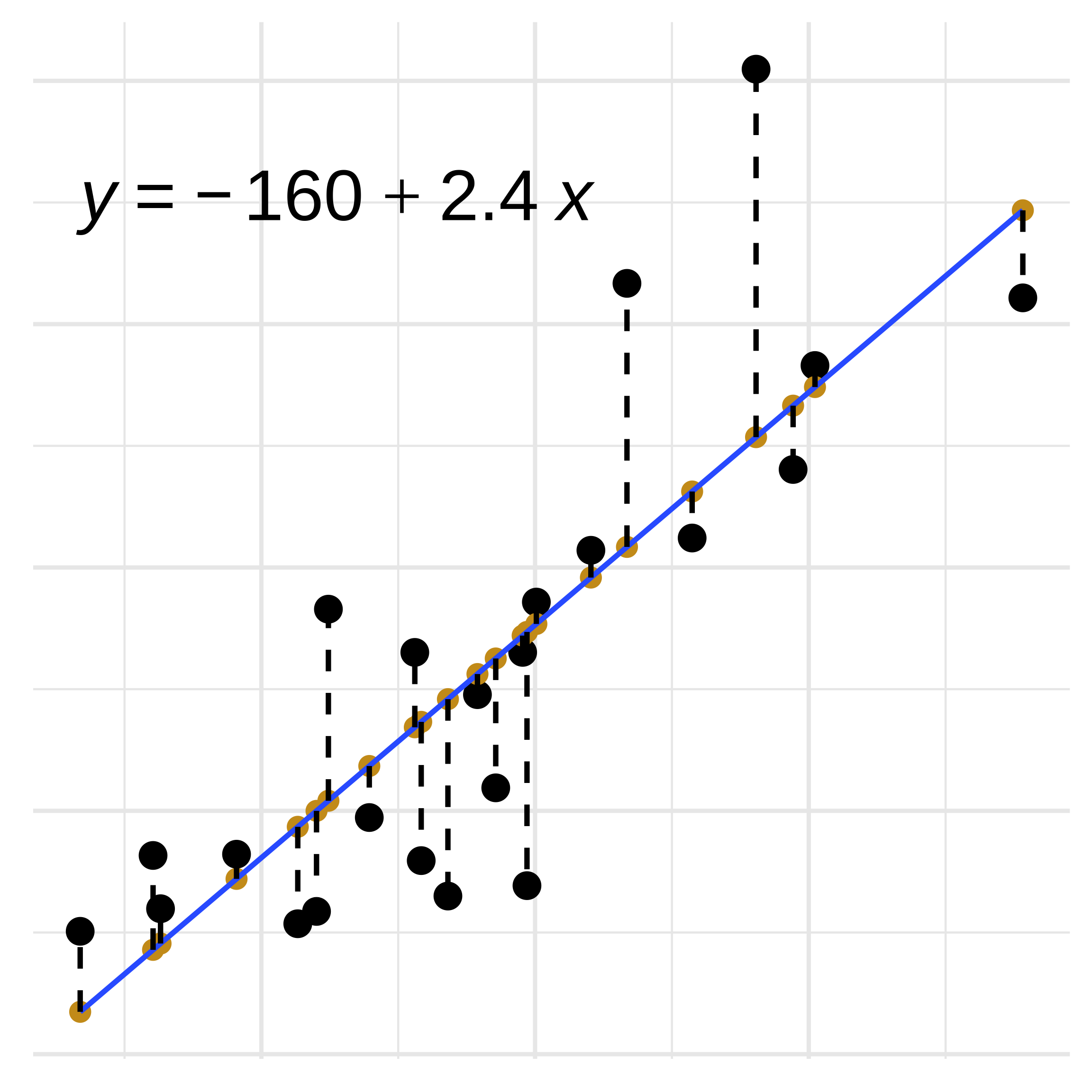
  • Residuals: \(r\)
  • Actual value: \(y\)
  • Predicted value (on the line): \(y_0\)
  • Formula: \(r = y-y_0\)
  • Smaller residuals = better model fit

Linear Regression: Model Fit

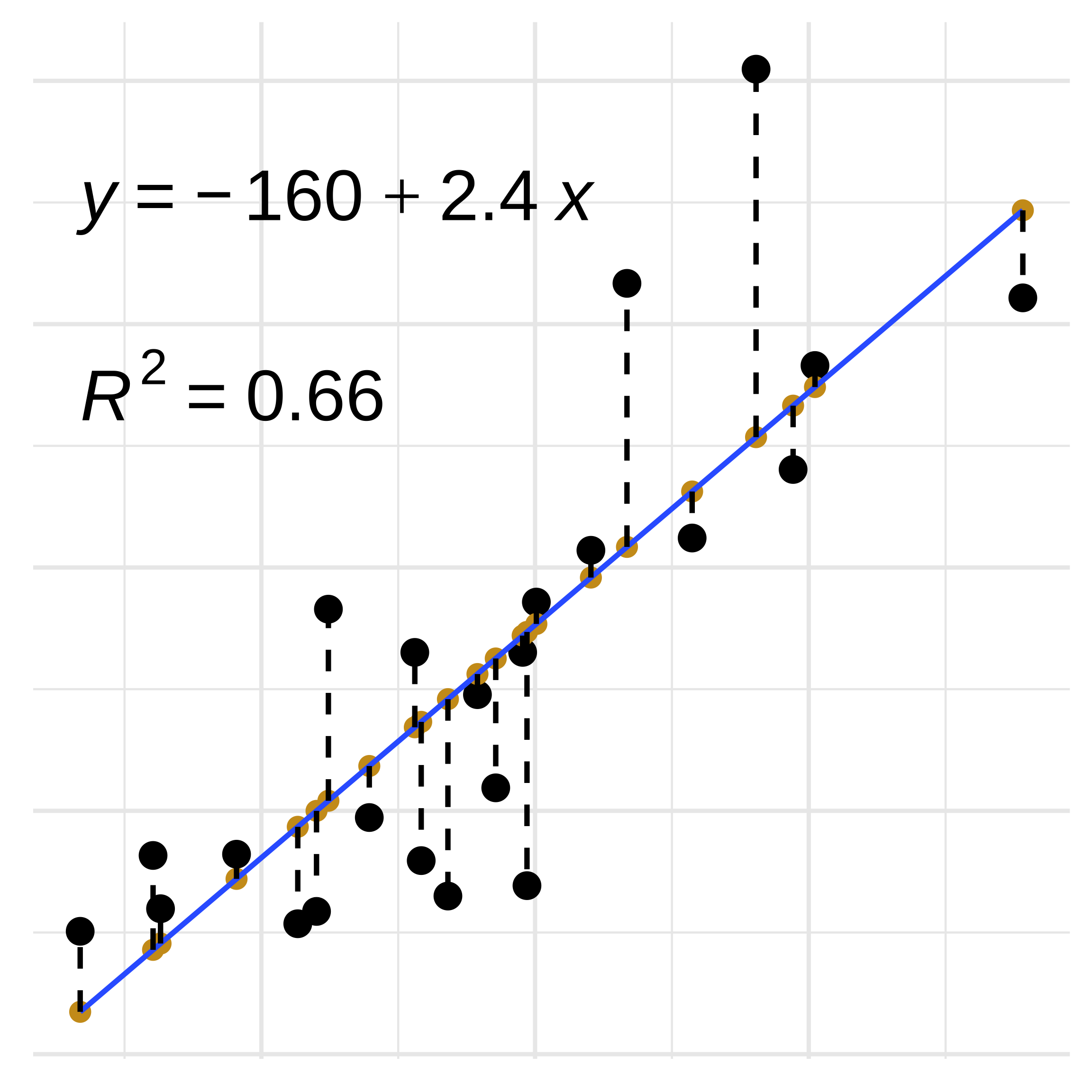
  • Model Fit: \(R^2\)
  • Mean of the response variable: \(\bar{y}\)
  • Sum of Squares Regression: \((y-\bar{y})^2\)
  • Sum of Squares Total: \((y_0-\bar{y})^2\)
  • \(R^2 = 1- \frac{(y-\bar{y})^2} {(y_0-\bar{y})^2}\)

Linear Regression: Model Fit

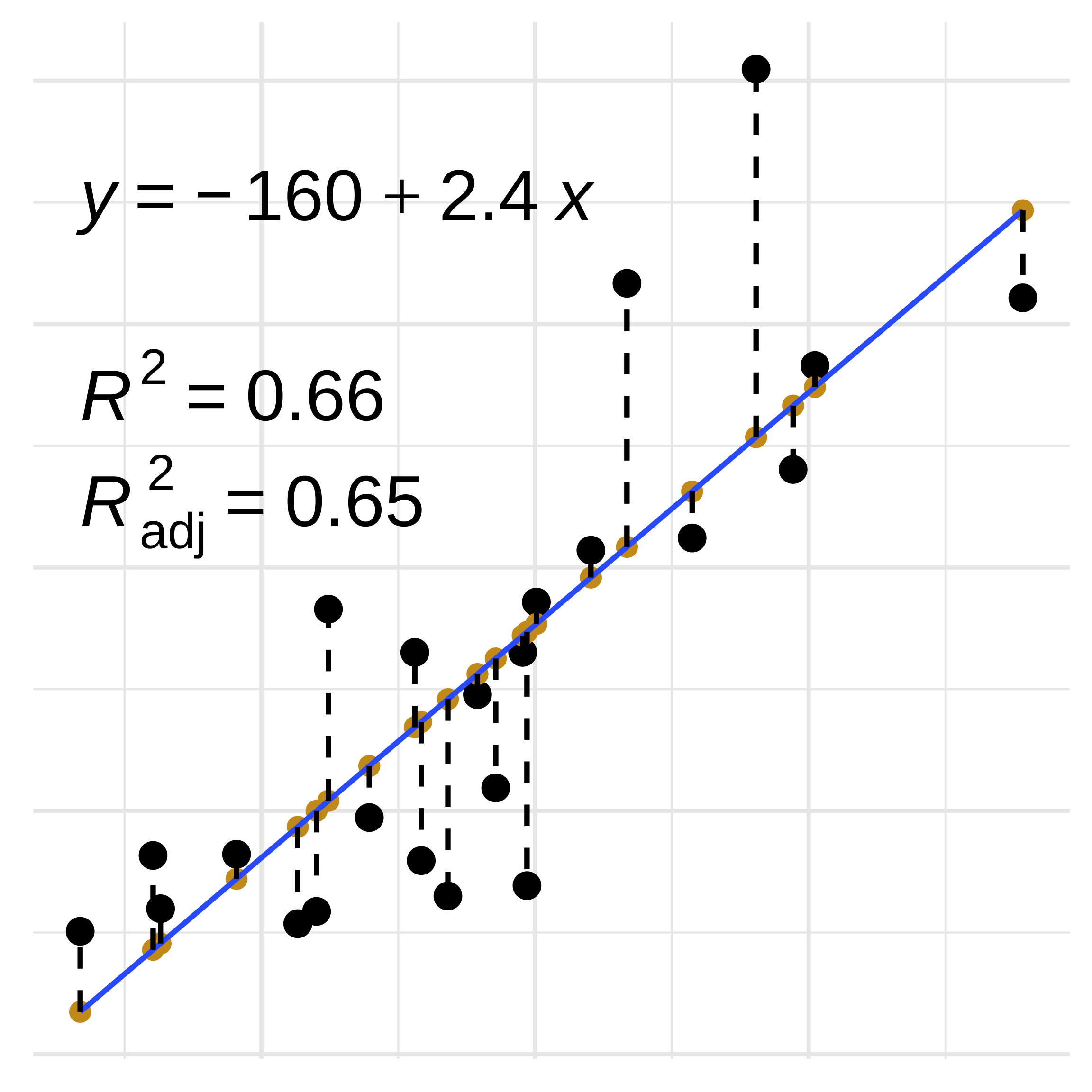
  • \(R^2_{adj}\) penalizes based on the number of predictor variables

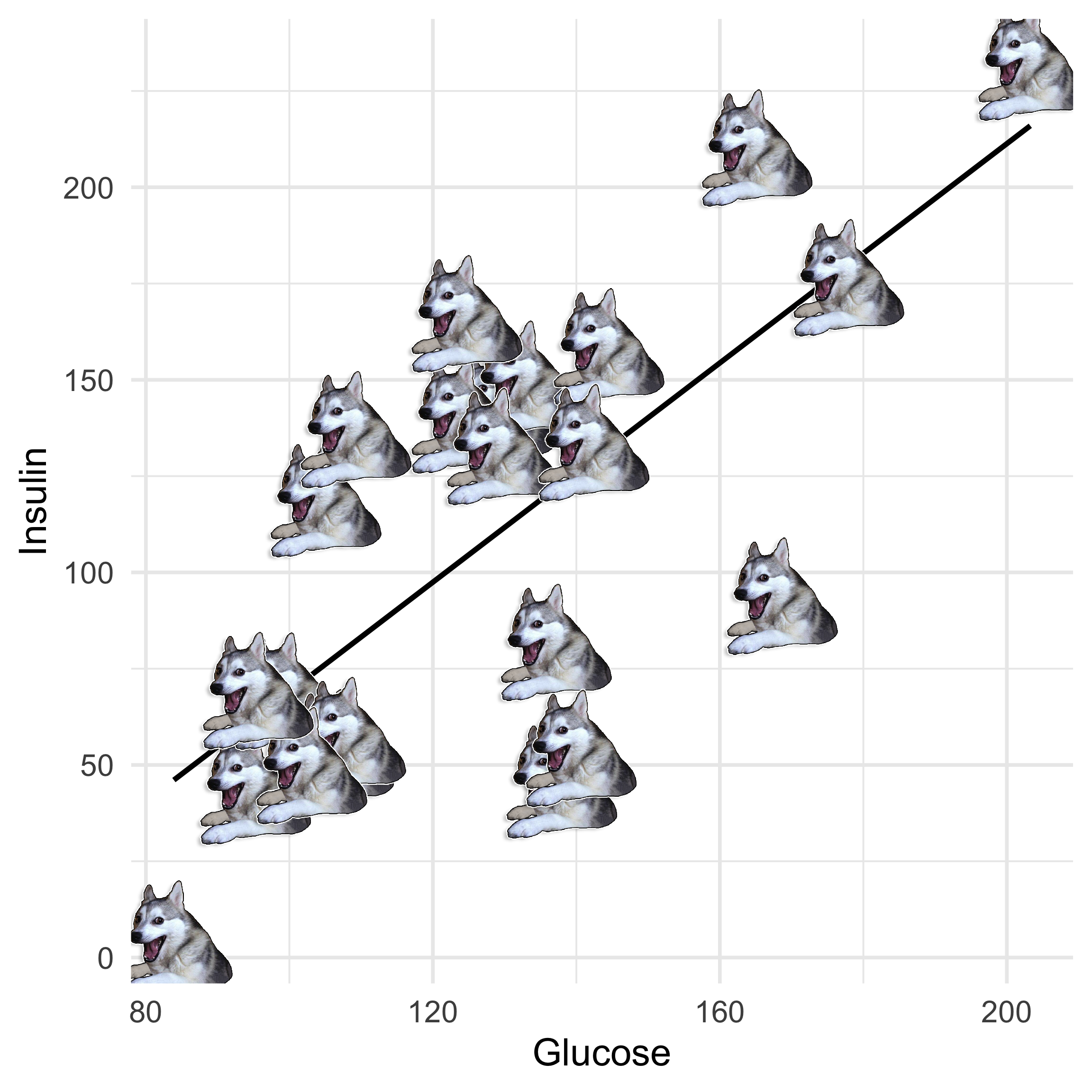
Linear Regression: Extrapolation

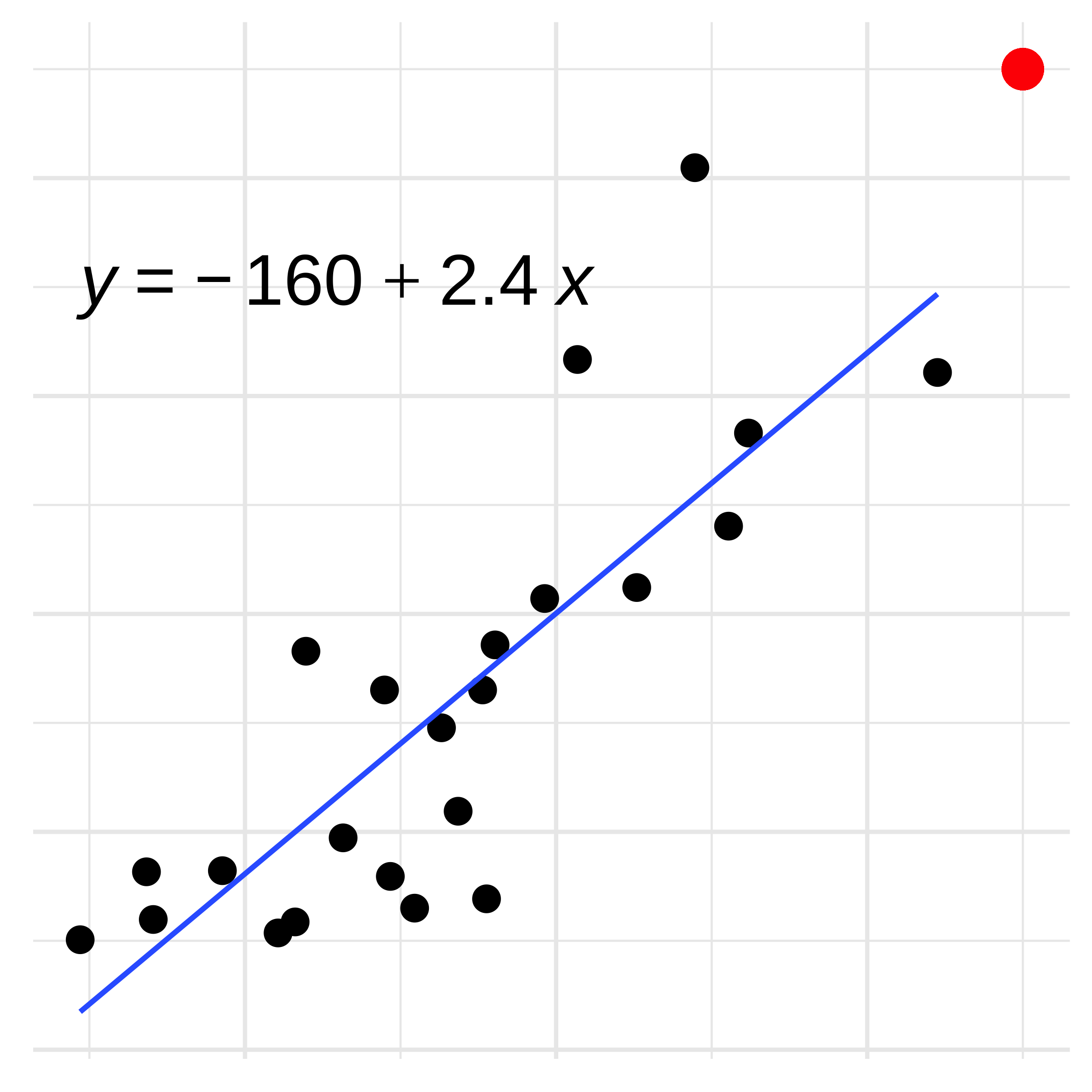
Can we make any inference about the new data point?

  • No, the point is outside of the bounds of our regression model.

  • This would be extrapolation, which is possible, but not advised.

Linear Regression: Extrapolation

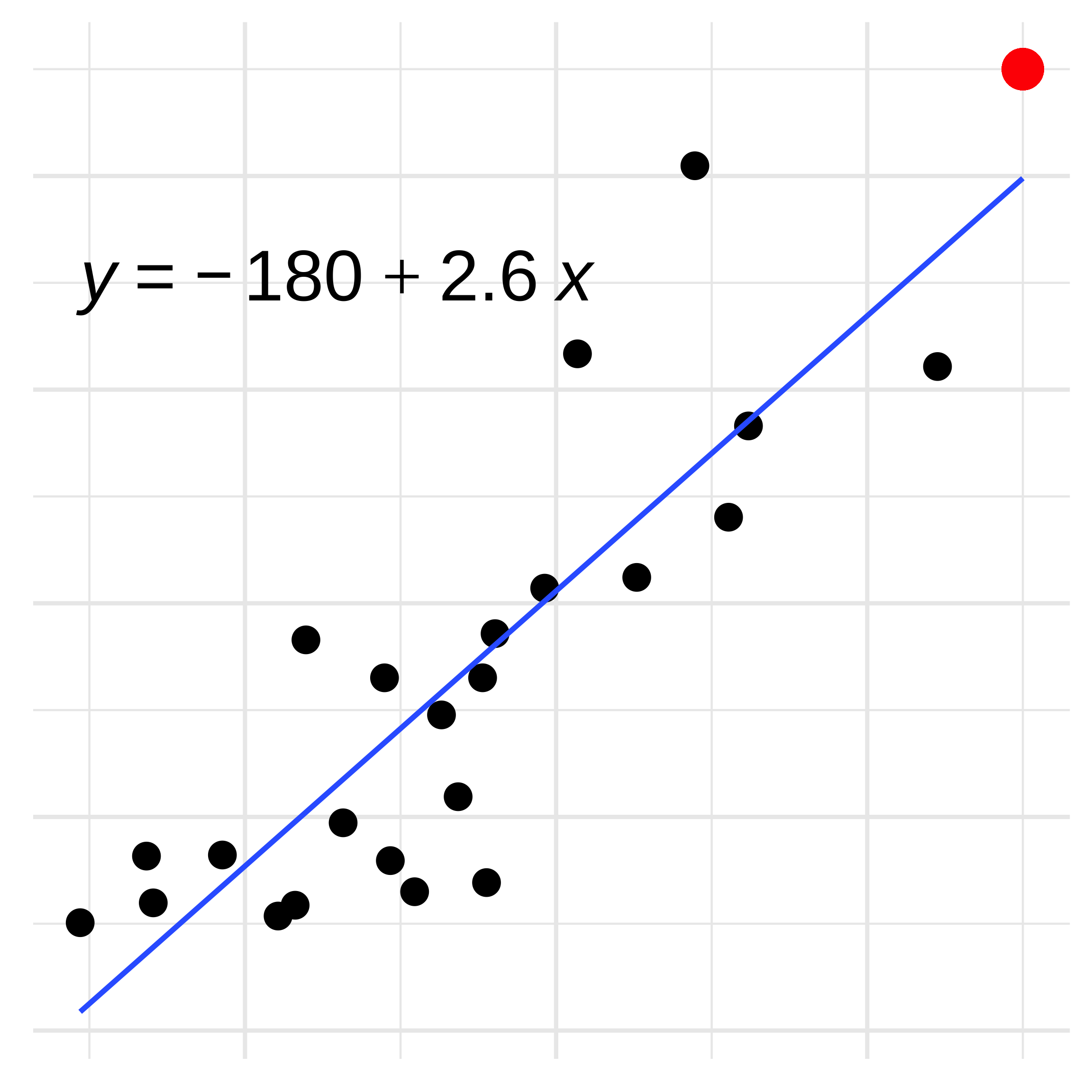
Instead you’d have to run a new model.

Correlation = Causation?

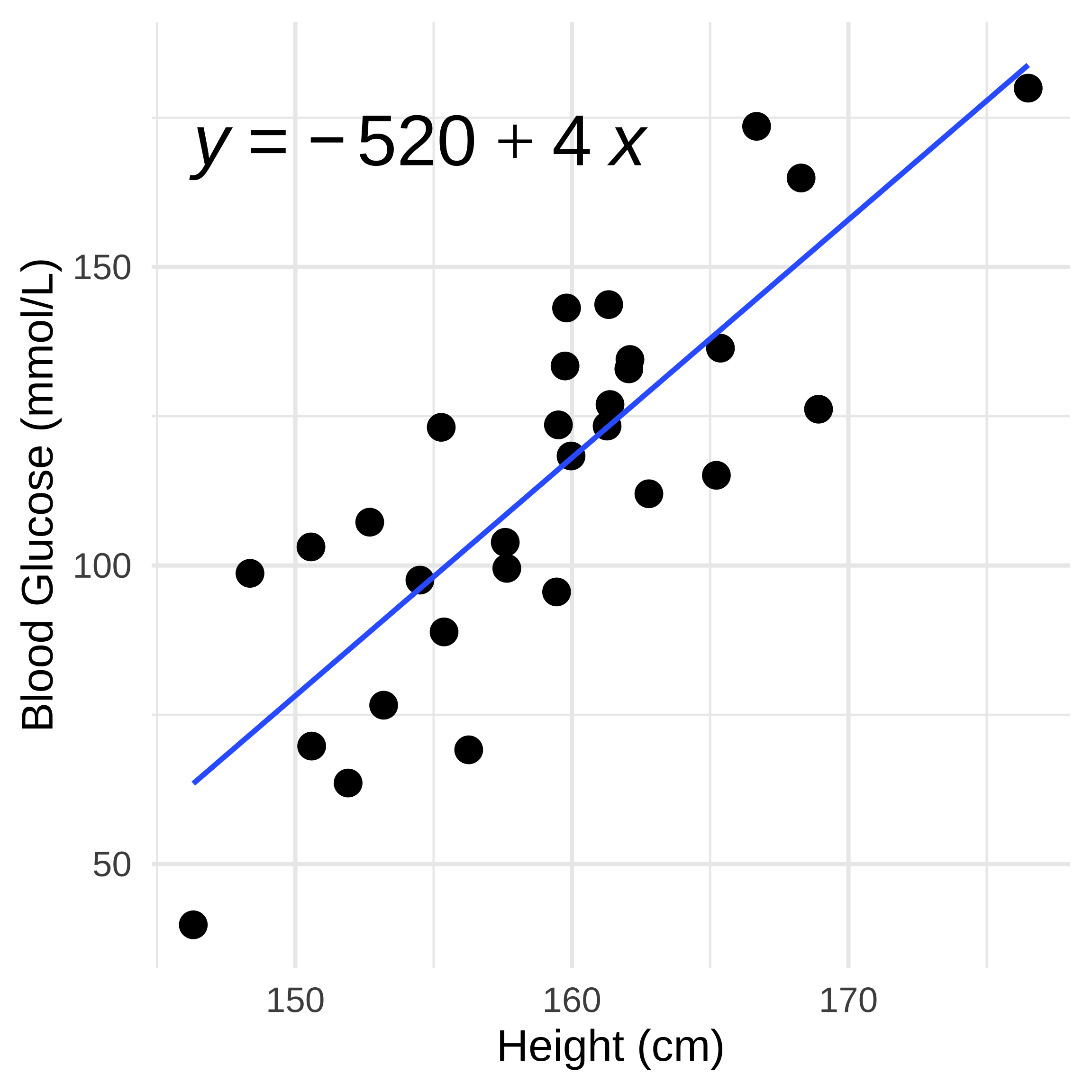
Is height (cm) related to Blood Glucose (mmol/L)?

  • Maybe…

  • There’s no information on how the data was collected or if this is experimental at all.

  • Bad Correlations…

Done!!

Artwork by @allison_horst